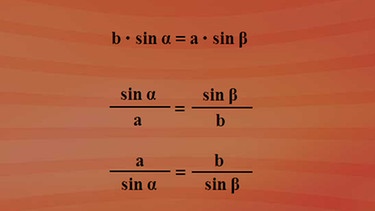Grundkurs Mathematik (14) 14.1. Spitzwinklige Dreiecke
Wie kann man Beziehungen zwischen Winkeln und Seiten im allgemeinen Dreieck finden? Ein Trick hilft weiter: eine Teilung in zwei rechtwinklige Dreiecke! Wir zeigen, wie es geht.
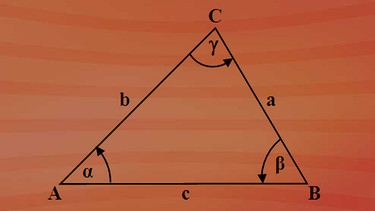
Kurz zur Wiederholung: Gegeben sei das spitzwinklige Dreieck ABC mit den Dreiecksseiten a, b und c und den Innenwinkeln alpha, beta und gamma. Ein Dreieck heißt spitzwinklig, wenn jeder Innenwinkel des Dreiecks kleiner als 90 Grad ist. Nebenbei noch ein anderer wichtiger Zusammenhang für die Winkel in Dreiecken: Die Winkelsumme der Innenwinkel eines jeden Dreiecks beträgt 180 Grad.
Der Trick mit dem Altbekannten
Wie können wir Beziehungen zwischen Winkeln und Seiten im allgemeinen Dreieck finden? Es gibt eine Methode, die wir schon öfters angewendet haben: Man versucht das Neue über etwas Altbekanntes herzuleiten. Und genau das werden wir jetzt tun.
Teilung in zwei rechtwinklige Dreiecke
Einzeichnen der Höhe
Durch das Einzeichnen der Dreieckshöhe auf der Seite c, also der Strecke AB, wird das allgemeine Dreieck ABC in zwei rechtwinklige Dreiecke geteilt. Diese beiden Teildreiecke wollen wir getrennt voneinander betrachten.
Kurzer Rückblick
Es entstehen zwei rechtwinklige Dreiecke.
Wissen Sie noch, welche Beziehungen zwischen Winkeln und Seiten im rechtwinkligen Dreieck Gültigkeit hatten?
Der Sinus eines Winkels war der Quotient aus der betreffenden Gegenkathete und der Hypotenuse. Der Kosinus der Quotient aus der betreffenden Ankathete und der Hypotenuse. Und der Tangens war Gegenkathete durch Ankathete.
Gegenkathete durch Hypotenuse ist der Sinus des betrachteten Winkels.
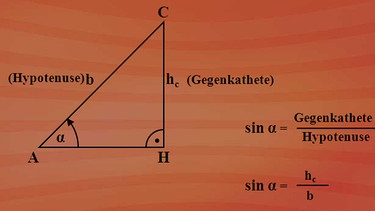
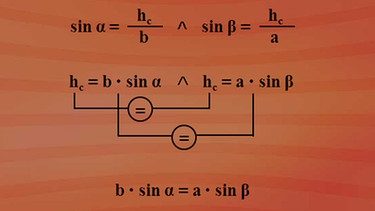
Betrachten wir das rechtwinklige Dreieck AHC. Vom Winkel Alpha aus gesehen, ist hc die Gegenkathete. Die Seite b ist Hypotenuse. Gegenkathete durch Hypotenuse ist der Sinus des betrachteten Winkels. Also Sinus Alpha ist hc durch b.
Soweit, was das Dreieck AHC betrifft. Wir haben aber bei der Aufspaltung in die Teilbereiche noch ein zweites Dreieck erhalten und auch dieses war rechtwinklig.
Die Beziehung zueinander der beiden Teildreiecke nutzen
Gegenkathete durch Hypotenuse ist der Sinus des betrachteten Winkels.
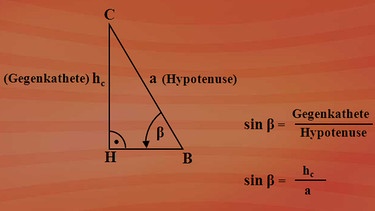
Das Dreieck HBC hat - vom Winkel Beta aus gesehen - die Seite hc als Gegenkathete und die Seite a als Hypotenuse. Und auch hier gilt: Gegenkathete durch Hypotenuse ist der Sinus des betrachteten Winkels. Also Sinus Beta ist hc durch a.
Klicken Sie bitte auf die Lupe
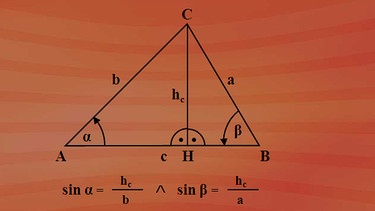
Die Seite hc ist aber in beiden Dreiecken identisch, denn hier haben wir die beiden Teildreiecke aufgespaltet.
Also könnten wir die beiden trigonometrischen Beziehungen zusammenfügen, sie bilden ein System.
Die Beziehung im ersten Teildreieck mit "Sinus Alpha ist gleich hc durch b" hat zur gleichen Zeit Gültigkeit wie die Beziehung im zweiten Teilbereich mit "Sinus Beta ist gleich hc durch a".
Die gemeinsame Strecke hc
Umformung der Terme
In beiden Gleichungen taucht die Seite hc auf. Wir werden nun versuchen, durch Elimination vonhc eine Beziehung zwischen Winkeln und Seiten in diesem allgemeinen Dreieck herzuleiten. Dazu formen wir beide Gleichungen nach hc um. Wir erhalten durch Multiplikation mit b bei der linken Gleichung "hc gleich b mal Sinus Alpha". Und durch Multiplikation mit a bei der rechten Gleichung "hc gleich a mal Sinus Beta".
Der Zusammenhang
Stimmen bei zwei Gleichungen die linken Seiten überein, müssen auch die rechten Seiten übereinstimmen. Und somit haben wir eine Beziehung zwischen Seiten und Winkeln in einem beliebigen Dreieck. Umgeformt geschrieben: "Sinus Alpha durch a ist gleich Sinus Beta durch b". Oder als Kehrbruch: "a zu Sinus Alpha ist gleich b zu Sinus Beta".