Beschleunigung Bewegungsgesetze
Von: Rolf Herold
Stand: 21.04.2020 |Bildnachweis
Schau dir zunächst das Video auf die folgenden Fragen hin an:
- Um welchen Zusammenhang geht es im Weg-Zeit-Gesetz und um welchen im Geschwindigkeits-Zeit-Gesetz?
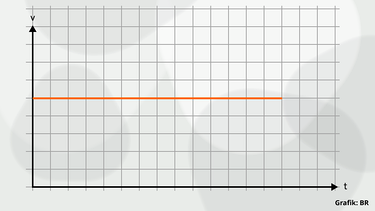
- Wie sieht das v-t-Diagramm einer Bewegung mit konstanter Geschwindigkeit aus und wie das einer gleichmäßig beschleunigten?
- Wie stellt man die Definitionsgleichung für a nach ∆ v um?
- Wann darf man v = at anwenden?
- Weißt du, was man unter "Anfangsgeschwindigkeit" versteht?
Weiter unten findest du die Antworten zu den Fragen und vertiefende Informationen.
Wenn wir in der Physik ein Diagramm verwenden, dann gibt es da eine Abmachung was die Reihenfolge der Achsen im Diagramm angeht: In einem A-B-Diagramm ist auf der Hochwertachse A und auf der Rechtswertachse B angegeben, denn das Diagramm stellt dar, wie A von B abhängig ist. Ein v-t-Diagramm hat also als Hochwertachse (y-Achse) die Geschwindigkeit v und als Rechtswertachse (x-Achse) die Zeit t.
Hier ein v-t-Diagramm bei konstanter Geschwindigkeit.
Das v-t-Diagramm bei gleichmäßiger Beschleunigung.
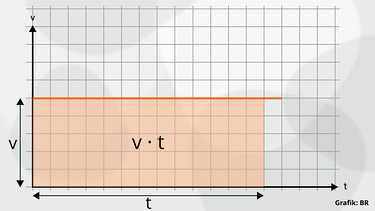
Hier siehst du, was die Formel s = v · t geometrisch betrachtet berechnet. Das Produkt v ∙ t entspricht dem Flächeninhalt des Rechtecks unter der zu v gehörigen waagrechten Linie bis zu einem bestimmten Zeitpunkt t.
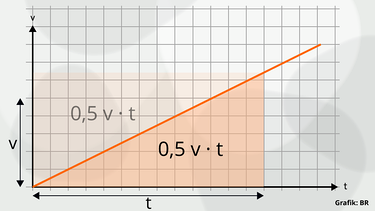
Und hier die geometrische Darstellung des Produkts ½ v ∙ t: Es entspricht dem Flächeninhalt des Dreiecks unter der zur beschleunigten Bewegung gehörigen Linie bis zu einem bestimmten Zeitpunkt t.
Zum Danebenlegen öffne das Bild mit rechter Maus + "Link in neuem Fenster öffnen".
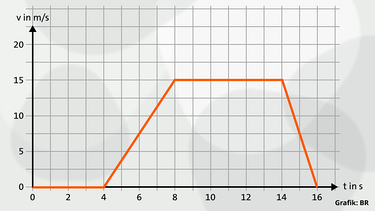
Ein Ausschnitt aus der Fahrt eines Autos im Berufsverkehr:
Wandern wir in diesem Diagramm von links nach rechts entlang der Linie, so sehen wir, dass in den ersten 4 s überhaupt nichts passiert. Warten im Stau - die Linie verläuft entlang der Zeitachse - v hat immer den Wert Null – Das Fahrzeug steht.
Losfahren: In den nächsten Sekunden steigt die Linie gerade an (weiter von links nach rechts). Die Geschwindigkeit steigt gleichmäßig bis auf 15 m/s. Das Fahrzeug wird immer schneller – es wird gleichmäßig beschleunigt.
Es fährt ein paar Sekunden: Von der 8. bis zur 14. Sekunde verläuft die Linie waagrecht. Der Wert für v ändert sich sechs Sekunden lang nicht. Das Fahrzeug fährt also gleichmäßig weiter.
Vollbremsung: Von der 14. bis zur 16. Sekunde sinkt die Linie wieder bis zur Achse ab. Die Geschwindigkeit sinkt auf Null. Das Fahrzeug wird gebremst. Es liegt eine Bewegung mit gleichmäßiger negativer Beschleunigung vor.
Die vier Phasen dieses Vorgang kann man nun im Hinblick auf die Bewegungsgesetze folgendermaßen einteilen:
| Zeit | Aktion |
|---|---|
| 1. bis 4. Sekunde | Stillstand → v = 0; a = 0 |
| 4. bis 8. Sekunde | Gleichmäßige Beschleunigung aus dem Stand → v = a t; s = 0,5 a t² (wobei t ab der 4. Sekunde gezählt wird) |
| 8. bis 14. Sekunde | Gleichförmige Bewegung ; a = 0
v = konstant; s = v t (wobei t ab der 8. Sekunde gezählt wird) |
| 14. bis 16. Sekunde | Gleichmäßige Beschleunigung mit Anfangsgeschwindigkeit und negativer Beschleunigung → v = v0 + a t; s = v0 t + 0,5 a t² (wobei t ab der 14. Sekunde gezählt wird) |
Frage
Um welchen Zusammenhang geht es im Weg-Zeit-Gesetz und um welchen im Geschwindigkeits-Zeit-Gesetz?
Antwort
Beim Weg-Zeit-Gesetz geht es darum, wie weit sich ein Körper bei einer beschleunigten Bewegung in einer bestimmten Zeit t bewegt hat. Beim Geschwindigkeits-Zeit-Gesetz geht es um die dabei erreichte Geschwindigkeit.
Frage
Wie sieht das v-t-Diagramm einer Bewegung mit konstanter Geschwindigkeit aus und wie das einer gleichmäßig beschleunigten?
Antwort
konstante Geschwindigkeit: waagrechte Linie
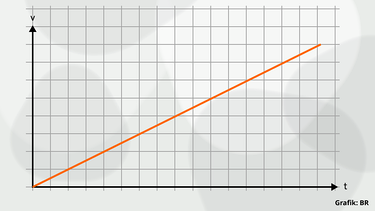
gleichmäßig beschleunigte Bewegung: eine ansteigende Gerade mit Beginn am Nullpunkt (siehe Seite weiter oben!)
Frage
Wie stellt man die Definitionsgleichung für a nach ∆ v um?
Antwort
a = ∆ v : ∆ t → ∆ v = a ∆ t
Frage
Wann darf man v = at anwenden?
Antwort
v = at gilt, wenn man eine beschleunigte Bewegung mit konstanter Beschleunigung a aus dem Stand hat. (Anfangsgeschwindigkeit = 0)
Frage
Weißt du, was man unter "Anfangsgeschwindigkeit" versteht?
Antwort
Der Begriff gehört zu beschleunigten Bewegungen. Die Anfangsgeschwindigkeit ist dabei die Geschwindigkeit, die ein Körper zu Beginn eines Beschleunigungsvorgangs hat.