GRIPS Mathe 16 Der Umfang
Den Umfang der Reithalle mit Schritten messen
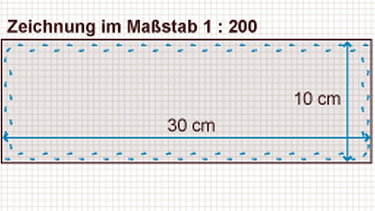
Matthias misst die Reithalle mit seinen Schritten aus.
Damit hat er automatisch auch den Umfang der Reithalle bestimmt.
Umfang
Der Umfang u ist die Summe aller Seitenlängen einer "geometrischen Figur".
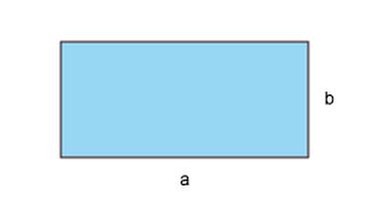
Schauen wir uns zuerst ein allgemeines Rechteck an:
Beispiel Rechteck
Rechteck
Der Umfang eines Rechtecks kann durch das "Aufklappen" aller Seiten ermittelt werden.
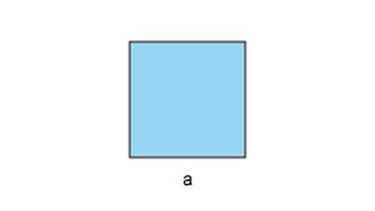
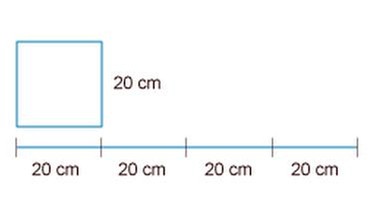
Eine Sonderform des Rechtecks ist das Quadrat:
Beispiel Quadrat
Quadrat
Der Umfang eines Quadrats kann ebenfalls durch das "Aufklappen" aller Seiten ermittelt werden.
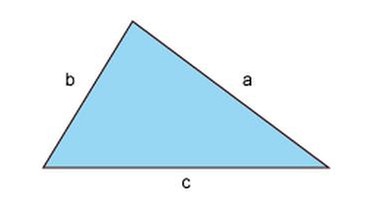
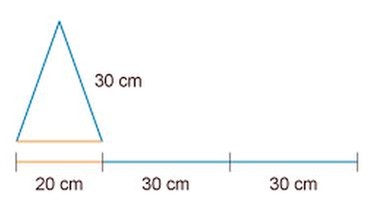
Und nun kommen wir noch zu einer ebenfalls recht häufigen Figur - dem Dreieck:
Beispiel Dreieck
Dreieck
Auch beim Dreieck kannst du alle drei Seiten "aufklappen", um den Umfang zu ermitteln.
