GRIPS Mathe 16 Der Flächeninhalt
Flächeninhalt mit Einheitsquadraten berechnen
Sebastian Wohlrab legt zusammen mit Matthias und Eve den Plan von der Pferdekoppel mit passenden Einheitsquadraten aus. Er verwendet dazu Quadrate mit der Seitenlänge 1 cm (Zentimeterquadrate).
Wie kann man mit diesen Einheitsquadraten den Flächeninhalt der Pferdekoppel herausbekommen? Die Lösung erfährst du in den nachfolgenden Grafiken:
Schritt 1 Fange an einer Ecke mit dem Auslegen an.
Flächeninhalt mit der Formel berechnen
Du kannst natürlich nicht bei jeder Flächenberechnung mit dem Auslegen von Quadraten beginnen. Mit der Rechtecks-Formel geht es schneller.
Sieh dir den Plan der Pferdekoppel noch einmal genau an. Er ist im Maßstab
1 : 500 gezeichnet. Wie lange und wie breit ist die Koppel aber in Wirklichkeit?
Plan der Pferdekoppel
Zuerst musst du mit dem Maßstab 1 : 500 rechnen, das heißt ein Zentimeter in der Zeichnung sind 500 cm in Wirklichkeit.
Du rechnest also vom Modell in die Wirklichkeit um.
1 : 500 bedeutet hier:
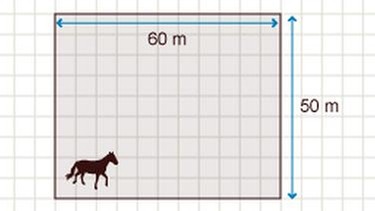
12 cm Länge auf dem Plan sind 6000 cm (12 · 500) in Wirklichkeit - also 60 m.
10 cm Breite auf dem Plan sind 5000 cm (10 · 500) in Wirklichkeit - also 50 m.
Die wirklichen Maße der Pferdekoppel sind 60 m (Länge) und 50 m (Breite). Jetzt ist es einfach den Flächeninhalt zu berechnen. Dazu verwendest du folgende Formel:
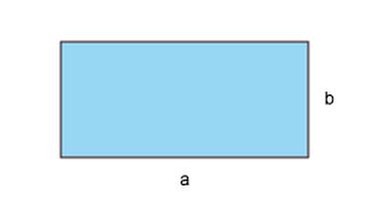
Flächeninhalt Rechteck
Formel
Den Flächeninhalt eines Rechtecks berechnest du mit dieser Formel:
Flächeninhalt = Länge · Breite
A = a · b
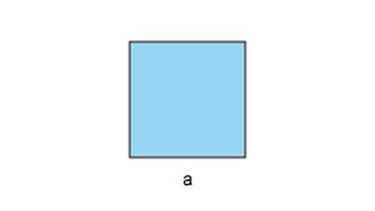
Den Flächeninhalt eines Quadrats berechnest du genauso:
Flächeninhalt Quadrat
Formel
Den Flächeninhalt eines Quadrats berechnest du mit dieser Formel:
Flächeninhalt = Länge · Breite
Da Länge und Breite gleich lang sind, gilt:
A = a · a
Durch Umstellen der Formel kannst du auch leicht die Länge oder die Breite eines Rechtecks oder Quadrats bestimmen, wenn du den Flächeninhalt kennst:
Länge oder Breite berechnen
Länge Rechteck
Gegeben: Flächeninhalt A = 1200 cm², Breite b = 40 cm
Gesucht: Länge a
Flächeninhalt = Länge · Breite
1200 cm² = a · 40 cm | : 40 cm
30 cm = a
Antwort: Die Seitenlänge a des Rechtecks beträgt 30 cm.