GRIPS Mathe 17 Flächenberechnung eines Parallelogramms
Die Flächenformel des Rechtecks kennst du schon. Diese Formel hilft dir dabei, den Flächeninhalt eines Parallelogramms zu berechnen. Denn jedes Parallelogramm lässt sich in ein flächengleiches Rechteck verwandeln. Probier es einfach aus. Du brauchst nur eine Schere, Stift und Papier.
Auf der vorherigen Seite hast du gesehen, wie du ein Parallelogramm konstruierst. Zeichne ein beliebiges Parallelogramm auf ein Blatt Papier und gehe dann so vor:
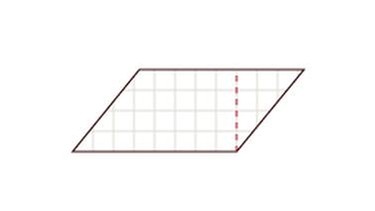
Parallelogramm in Rechteck umwandeln
Schritt 1
Schneide das Parallelogramm aus.
Flächeninhalt Parallelogramm
Formel: Flächeninhalt Parallelogramm
Die Flächenformel für das Parallelogramm lässt sich aus der Flächenformel für das Rechteck ableiten (siehe oben):
Formel Rechteck: AR = a · b
Formel Parallelogramm: AP = g · h
Beispiel für die Flächenberechnung eines Parallelogramms:
AP = g · h
AP = 12 cm · 7 cm
AP = 84 cm²
Flächeninhalt des Gartenbeets
Das Gartenbeet soll mit Silberrauten bepflanzt werden. Das Beet ist 4 m lang und 2 m breit. Pro Quadratmeter sind 3 Stück vorgesehen. Wie viele Pflanzen sind nötig?
Rechenschritte
Gegeben / Gesucht
Gegeben:
Grundseite g = 4 m
Höhe h = 2 m
Gesucht:
Fläche A des Beetes