GRIPS Mathe 18 Regelmäßiges Fünfeck

In vielen Abschlussprüfungen musst du regelmäßige Vielecke konstruieren. Am Beispiel der Qualiprüfung 2009 zeigen wir dir, wie das geht. Konstruiert werden soll ein regelmäßiges Fünfeck mit Hilfe des Bestimmungsdreiecks.
Qualiprüfung 2009 - Konstruktionen
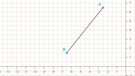
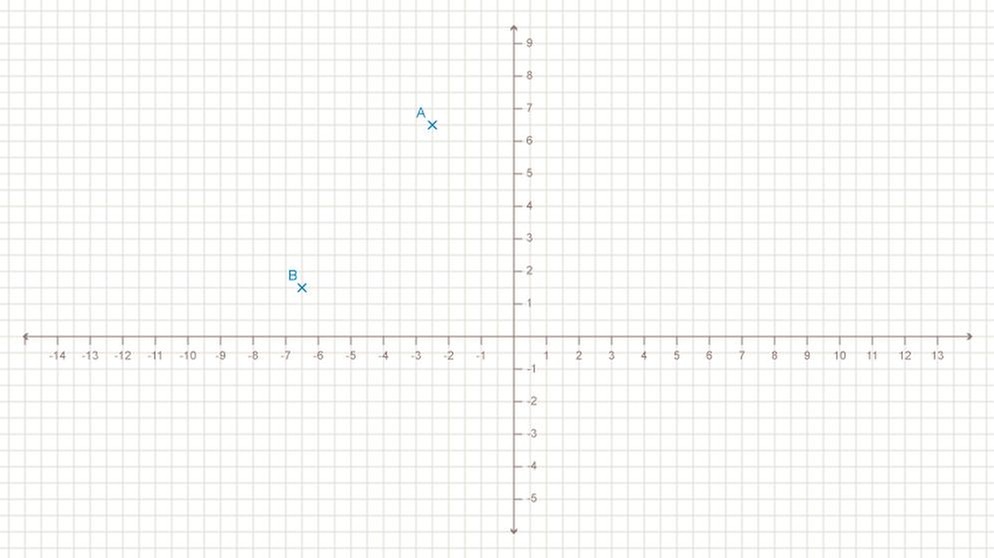
Die Punkte A (-2,5/6,5) und B (-6,5/ 1,5) sind benachbarte Eckpunkte eines regelmäßigen Fünfecks. Zeichne in einem Koordinatensystem mit der Einheit 1 cm die Strecke [AB]. Finde den Mittelpunkt M des Fünfecks, indem du das Bestimmungsdreieck BMA zeichnest. Zeichne das Fünfeck.
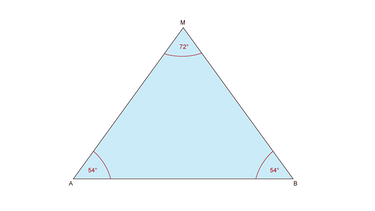
Zur Lösung der Aufgabe berechnest du zuerst die Größe der drei Winkel des Bestimmungsdreiecks:
Winkel Bestimmungsdreieck
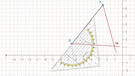
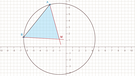
Nachdem du die Winkel des Bestimmungsdreiecks berechnet hast, kannst du das Fünfeck konstruieren: