GRIPS Mathe 18 Flächenberechnung von Vielecken

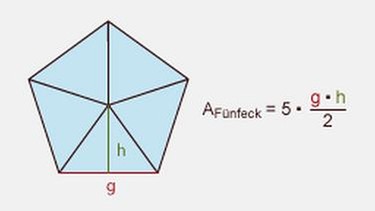
Ein regelmäßiges Fünfeck besteht aus fünf gleich großen Bestimmungsdreiecken.
Jedes dieser Dreiecke hat einen Mittelpunktswinkel von 72°:
360° : 5 = 72°.
Flächeninhalt Vieleck
Möchtest du den Flächeninhalt eines Vielecks berechnen, berechnest du den Flächeninhalt des Bestimmungsdreiecks und multiplizierst diesen mit der Anzahl der Bestimmungsdreiecke im Vieleck bzw. mit der Anzahl der Ecken.
Für den Flächeninhalt eines Fünfecks bedeutet das: Flächenformel Dreieck mal 5.
Hier siehst du, mit welchen Formeln du den Flächeninhalt eines reglemäßigen Fünfecks, eines regelmäßigen Sechsecks und eines regelmäßigen Achtecks berechnest:
Formeln: Flächeninhalt regelmäßige Vielecke
Regelmäßiges Fünfeck
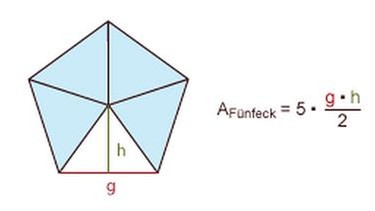
Ein Fünfeck besteht aus fünf Dreiecken.
Um den Flächeninhalt eines Fünfecks zu berechnen, multiplizierst du die Flächenformel für das Dreieck einfach mit 5.
Hinweis: Möchtest du ein Fünfeck zeichnen, berechnest du seinen Mittelpunktswinkel: 360° : 5 = 72°.
Regelmäßiges Sechseck
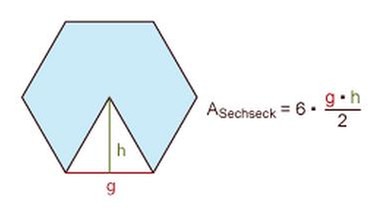
Ein Sechseck besteht aus sechs Dreiecken.
Um den Flächeninhalt eines Sechsecks zu berechnen, multiplizierst du die Flächenformel für das Dreieck mit 6.
Hinweis: Der Mittelpunktswinkel eines Sechsecks beträgt: 360° : 6 = 60°.
Regelmäßiges Achteck

Ein Achteck besteht aus acht Dreiecken.
Um den Flächeninhalt eines Achtecks zu berechnen, multiplizierst du die Flächenformel für das Dreieck mit 8.
Hinweis: Der Mittelpunktswinkel eines Achtecks beträgt: 360° : 8 = 45°.
Beispiel: Flächeninhalt Fünfeck
Gegeben / Gesucht

Gegeben:
Grundseite g des Bestimmungsdreiecks = 70 cm.
Höhe h des Bestimmungsdreiecks = 50 cm.
Gesucht:
Flächeninhalt A des Fünfecks
Lösung

Lösung:
Gegebene Werte in die Formel einsetzen und den Flächeninhalt des Fünfecks berechnen.
Antwort: Der Flächeninhalt des Fünfecks ist 8750 cm².