GRIPS Mathe 29 Der Satz des Pythagoras
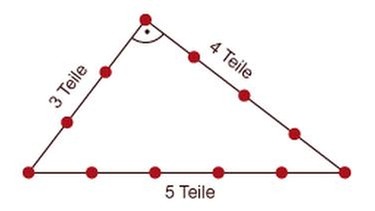
Auf der vorherigen Seite hast du gesehen, wie du mit Hilfe eines Knotenseils einen rechten Winkel legen kannst. Jetzt fehlt noch der Beweis, warum das so ist.
Dieser Beweis ist einem Griechen namens Pythagoras gelungen. Deswegen wurde der Lehrsatz auch "Satz des Pythagoras" genannt.
Der Satz des Pyhtagoras
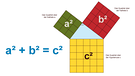
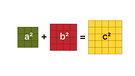
Der Satz des Pythagoras besagt, dass in einem rechtwinkligen Dreieck die Summe der Flächeninhalte der beiden Kathetenquadrate genauso groß ist, wie der Flächeninhalt des Hypotenusenquadrats.
Was heißt das? Sieh dir dazu die nachfolgenden Abbildungen an und lies dir die Texte darunter durch. Hinweis: Um den Text lesen zu können, muss du ihn erst aufklappen.
Der Satz des Pythagoras Der Satz des Pythagoras sagt, dass das gelbe Quadrat genauso groß ist wie das rote und grüne Quadrat zusammen. Oder anders ausgedrückt: Das Quadrat über der Hypotenuse c ist genauso groß wie das Quadrat über der Kathete a plus das Quadrat über der Kathete b, also: a² + b² = c².
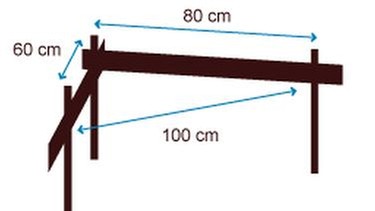
Mit Hilfe der Abbildungen hast du gelernt, was der Satz des Pythagoras ist und wie man ihn mit Quadraten beweisen kann. Der Satz des Pythagoras funktioniert aber auch, wenn du Zahlen einsetzt:
Beispiele für den Satz des Pythagoras
Beispiel 1
Das Knotenseil besteht aus 3 bzw. 4 Teilen an den Katheten und aus 5 Teilen an der Hypotenuse.
Setzt du diese Zahlen in den Satz des Pythagoras ein, gilt:
a² + b² = c²
3² + 4² = 5²
9 + 16 = 25
Das Beispiel zeigt, dass die Rechnung stimmt und der Satz des Pythagoras wahr ist.
