GRIPS Mathe 29 Anwendungsaufgaben

Mit dem Satz des Pythagoras kannst du die Seitenlängen eines rechtwinkligen Dreiecks berechnen. Dafür müssen zwei der drei Seitenlängen gegeben sein. Wir zeigen dir für jede Dreiecksseite ein Beispiel:
Aufgabe 1:
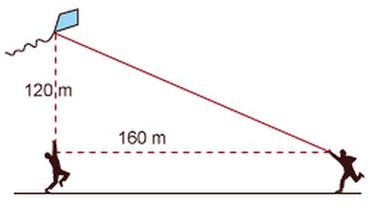
Markus und Andreas lassen einen Drachen steigen. Wie lange ist die Schnur des Drachens?
Lösung:
Die Schnur liegt dem rechten Winkel gegenüber und ist die längste der drei Seiten des Dreiecks. Sie bildet daher die Hypotenuse. Der Satz des Pythagoras lautet: a² + b² = c². Die Seite c steht für die Hypotenuse, daher ist also c gesucht.
Wenn du die gegebenen Streckenlängen (Katheten) a = 120 und b = 160 einsetzt, ergibt sich folgende Rechnung:
a² + b² = c²
120² + 160² = c²
14400 + 25600 = c²
40000 = c² | √
200 = c
Antwort: Die Schnur hat eine Länge von 200 m.
Aufgabe 2:

Markus möchte wissen, wie hoch der Drachen über seinem Kopf schwebt.
Lösung:
Diesmal ist die Länge der Schnur gegeben: c = 200 m. Außerdem ist die Länge einer der Katheten gegeben: b = 160 m. Gesucht ist die Länge der Seite a.
a² + b² = c²
a² + 160² = 200²
a² = 200² - 160²
a² = 40000 - 25600
a² = 14400 | √
a = 120
Antwort: Der Drache fliegt 120 m über Markus Kopf.
Aufgabe 3:

Wie weit stehen Markus und Andreas voneinander entfernt?
Lösung:
Auch hier ist die Länge der Schnur bekannt: c = 200 m. Außerdem ist eine der Katheten gegeben: a = 120 m. Gesucht ist die Länge der Seite b.
a² + b² = c²
120² + b² = 200²
b² = 200² - 120²
b² = 40000 - 14400
b² = 25600 | √
b = 160
Antwort: Markus und Andreas stehen 160 m voneinander entfernt.