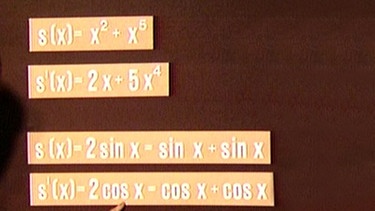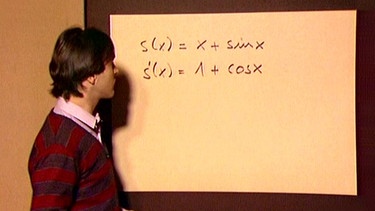Ableitungsregeln Differenzieren einer Summe von Funktionen
Wie funktioniert das Differenzieren einer Summe von Funktionen? Das erfahren Sie hier.
An zwei Beispielen wird nun das Differenzieren einer Summe von Funktionen gezeigt:
Differenzieren einer Summe von Funktionen
s(x) = x2 + x5 =>
s’(x) = 2x + 5x4 s(x) =
2·sin x = sin x + sin x =>
s’(x) = 2·cos x = cos x + cos x
Aufstellen der Hypothese
Aufstellen der Hypothese
Nun wird als Fortsetzung des o.g. Verfahrens die Hypothese aufgestellt: s(x) = x + sin x => s’(x) = 1 + cos x
Grafische Darstellung
Grafische Darstellung von s(x) = x + sin x
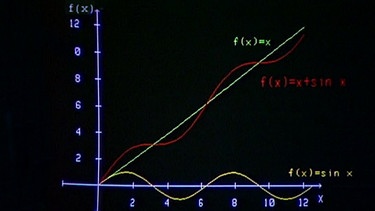
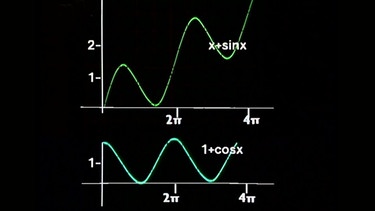
Am Rechner wird zunächst der Graph der Funktion s(x) = x + sin x dargestellt, es zeigt sich eine schräg nach oben verlaufende Sinuslinie.
Verlauf der Eingangs- und Ausgangsspannung des C-R-Glieds
Ein Versuch mit dem Funktionsgenerator, der diesmal eine Spannung U(t) = U·t + U·sin ωt erzeugt, zeigt am Eingang die vom Rechner bekannte ansteigende Sinuslinie und am Ausgang tatsächlich eine um den Summanden 1 nach oben verschobene Cosinuslinie, d.h. die Hypothese wurde experimentell betätigt. Auch wenn der Zeitanstieg bei der Eingangsspannung geändert wird, ändert sich der Summand bei der Cosinusspannung am Ausgang proportional.