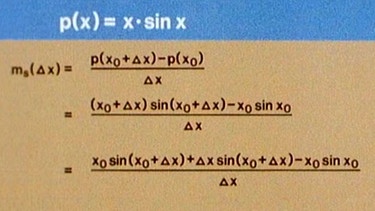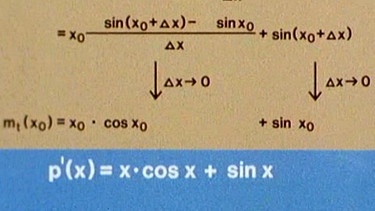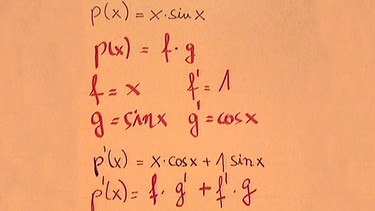Es soll die Ableitung eines Produkts von zwei Funktionen untersucht werden:
f(x)·g(x).

Faktorweises Differenzieren führt zum falschen Ergebnis

Wie die Rechnung an der Tafel zeigt, führt faktorweises Differenzieren zum falschen Ergebnis. Man kann aber zunächst die Exponenten zusammenfassen und dann differenzieren, das führt zum richtigen Ergebnis: f’(x²·x³) = 5x⁴

Grafische Darstellung der Funktion f(x) = x·sin x - klicken Sie bitte auf die Lupe.

Wie aber lässt sich z.B. die Funktion x·sin x ableiten? Den Graphen der Funktion kann man sich wieder am Rechnerbildschirm ansehen. Die Differenzierschaltung am Funktionsgenerator zeigt am Ein- und Ausgang einen ähnlichen verlauf, aber eine Ableitungsfunktion lässt sich so nicht ermitteln.

Ermittlung der Ableitung durch Grenzwertbildung in mehreren Stufen, Teil 1 - klicken Sie bitte auf die Lupe.

Hier muss nach den Regeln der Grenzwertbildung in mehreren Stufen die Ableitung ermittelt werden.

Ermittlung der Ableitung durch Grenzwertbildung in mehreren Stufen, Teil 2 - klicken Sie bitte auf die Lupe.

Man erhält als Ergebnis: p(x) = x·sin x => p’(x) = x·cos x + sin x.

Betrachtung der Funktion und ihrer Ableitung

Betrachtung der Funktion und ihrer Ableitung

Nachdem die elektronische Schaltung hier nicht zum Ziel führt, lässt sich die allgemeine Regel aber durch Betrachtung der Funktion und ihrer Ableitung doch ermitteln:
p(x) = f · g => p’(x) = f ·g’ + f ’·g

Zusammenstellung der ermittelten Ableitungsfunktionen

Auf die Herleitung der Ableitung von 1/f(x) schließlich wird aus Zeitgründen verzichtet, sie wird nur mitgeteilt:
f(x) = 1/x => -f’(x)/f²(x)