Extremwertaufgaben 2 Mathematische Lösung
Löst man die Frage nicht experimentell, sondern mathematisch, so handelt es sich um eine Extremwertaufgabe. Die gehen wir nun an.
Die ersten zwei Schritte zur Lösung einer Extremwertaufgabe
Das nötige Vorgehen wird anhand der vorher genannten Aufgabe Schritt für Schritt erklärt:
1. Welche Größe soll ein Minimum oder Maximum werden?
2. Diese Größe muss als Funktion von Variablen dargestellt werden.
Gesucht wird der Winkel alpha
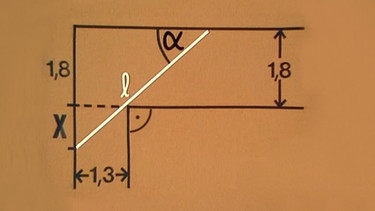
Zunächst werden relevante Größen, wie Winkel α des Stabes gegenüber der Wand oder die Breite der beiden Gänge, 1,8 m und 1,3 m, erfasst. Dass die beiden Gänge einen Winkel von 90º einschließen, wird vorausgesetzt und die Dicke des Stabes gegenüber den anderen Strecken vernachlässigt.
Modellskizze mit den relevanten Größen
Schließlich findet man noch eine Länge x, die vom Ende des Stabes und der Verlängerung der unteren Gangwand bestimmt wird.
Extremalbedingung für den Winkel alpha
Der Sinus des Winkels α ist gleich der Summe von 1,8 m plus x geteilt durch die Stablänge l, sin α = (1,8 + x)/l . Umgeformt ergibt sich l = (1,8 + x)/sin α = 1,8/sin α + x/sin α . Diese Funktion l(sin α) ist die gesuchte Extremalbedingung. Allerdings enthält diese Funktion außer der gesuchten Größe l auch noch die Variable x, für diese muss eine weitere Bedingung gefunden werden.
Es folgen also zwei weitere Lösungsschritte ...