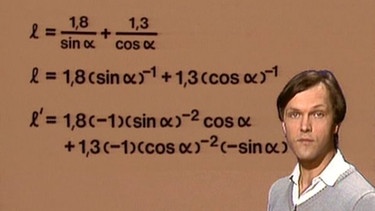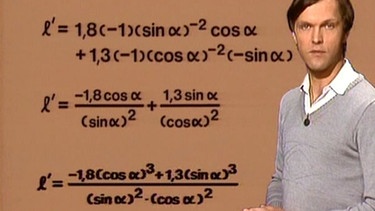Schritt 3 und 4 zur Lösung der Extremwertaufgabe

Es folgen also zwei weitere Lösungsschritte:

3. Ist diese Größe von mehr als einer Variablen abhängig?

4. Zwischen diesen Variablen muss eine Beziehung gesucht werden.

Die Strecke x ist die Gegenkathete zum Winkel alpha.

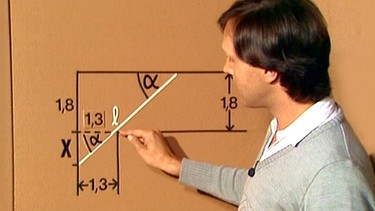
Die Strecke x ist die Gegenkathete zum Winkel α, der in dem kleinen rechtwinkligen Dreieck nochmals auftritt.

Aufstellen der Nebenbedingung

Die Beziehung zum Winkel α lautet dann tan α  = x/1,3 bzw. x = 1,3tan α. Dies ist die gesuchte Nebenbedingung.

Setzt man 1,3tan α statt x in die Funktion l = 1,8/sin α + x/sin α ein, so ergibt sich
l = 1,8/sin α + 1,3tan α/sin α . Mit der bekannten Beziehung tan α  = sin α/cos α erhält man schließlich
l(a) = 1,8/sin α + 1,3/cos α .
Dieses Einsetzen entspricht Schritt 5:

Schritt 5

Schritt 5 zur Lösung der Extremwertaufgabe

5. Mit Hilfe der Nebenbedingung wird die Extremalbedingung so umgerechnet, dass die Größe, die ein Extremum annehmen soll, als Funktion von nur einer Variablen erscheint.
Durch Ableiten der Funktion lässt sich nun das Extremum, in diesem Fall ein Minimum, ermitteln. Das entspricht Schritt 6:

Schritt 6

Schritt 6 zur Lösung der Extremwertaufgabe

6. Von der durch die Extremalbedingung dargestellten Funktion wird die 1. und 2. Ableitung gebildet.

Die Extremalfunktion wird umgeformt und ihre 1. Ableitung gebildet

Dazu wird die Funktion l(a) umgeformt, um die Ableitungsschritte besser nachvollziehen zu können:
l(a) = 1,8(sin α)^-1 + 1,3(cos α)^-1 . Die Ableitung dieser zusammengesetzten Funktionen erfolgt nach der Kettenregel und man erhält für die 1. Ableitung:

l’(a) = 1,8(-1)(sin α)^-2 cos α + 1,3(-1)(cos α)^-2(-sin α) .

Die 1. Ableitung wird weiter umgeformt um die Nullstellen leichter zu finden

Umgeformt und zusammengefasst erhalten wir: l’(a) = -1,8cos α/(sin α)2 + 1,3sin α/(cos α)²

Bildet man nun einen gemeinsamen Nenner, so ergibt sich schließlich

l’(a) = (-1,8(cos α)³ + 1,3(sin α)³/(sin α)²·(cos α)²

Um nun das Extremum zu finden, machen wir den 7. Schritt ...