Extremwertaufgaben 2 Weiteres Beispiel
Die vorgestellte Lösungsstrategie soll nun in einer zweiten Aufgabe angewendet werden.
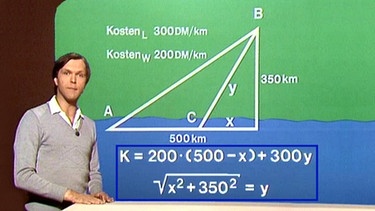
Eine Fabrik in A will Waren zu einem Kunden in B liefern. Auf dem Landweg fallen Transportkosten von 300 DM/km an, einen Teil der Strecke könnte man aber auch auf einer nahe gelegenen Wasserstraße zurücklegen, wo nur 200 DM/km anfallen. Wie die Abbildung zeigt, sind der reine Landweg, aber auch viele Kombinationen von Wasser- und Landtransport möglich. Entscheidend ist nun, welche Kombination am preisgünstigsten ist.
Eine Skizze verdeutlicht die Situation: Auf dem Wasser können maximal 500 km zurückgelegt werden, die kürzeste Strecke von der Wasserstraße zum Kunden beträgt 350 km. Der Punkt des Übergangs vom Wasser- zum Landtransport heißt C, die Strecke 500 km – AC wird x genannt und die Strecke CB heißt y . Die Extremalfunktion für die Kosten lautet K(x) = 200(500-x) + 300y . Die zweite Variable y lässt sich nach dem Satz von Pythagoras durch die Beziehung (x2 + 3502]0,5 = y ersetzen, das ist die Nebenbedingung.
Wird (x2 + 3502]0,5 in die Funktionsgleichung eingesetzt, so erhalten wir K(x) = 200(500-x) + 300(x2 + 3502]0,5.
Die 1. Ableitung K’(x) errechnet sich dann zu K’(x) -200+ 300/(x2 + 3502]0,5.
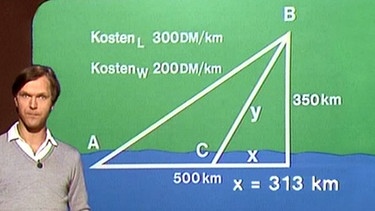
Für K’(x) = 0 bzw. 0 = -200+ 300/(x2 + 3502]0,5 erhalten wir den Wert x = 313.
Aus dieser Größe lassen sich dann auch der komplette Transportweg ACB sowie die Kosten für die Teilstrecken AC und CB berechnen.
Testen Sie Ihr Wissen!