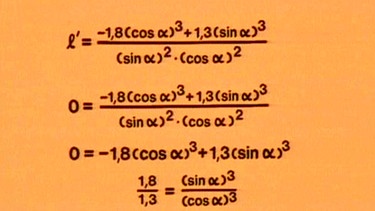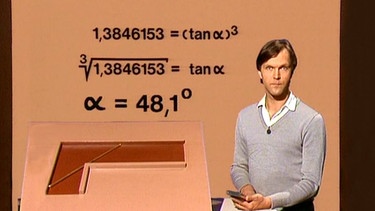Extremwertaufgaben 2 Das Extremum ermitteln
Wie kann man nun das Extremum ermitteln? Das erfahren Sie hier.
Die 1. Ableitung wird Null gesetzt. Die entstandene Gleichung wird gelöst.
Die weitere Rechnung sieht dann so aus: 0 = (-1,8(cos α)3+ 1,3(sin α)3/(sin α)2·(cos α)2
Da der Nenner nicht unendlich werden kann, muss der Zähler gleich Null sein:
0 = (-1,8(cos α)3+ 1,3(sin α)3 => 1,8/1,3 = (sin α)3/(cos α)3, 1,8/1,3 als Dezimalbruch ergibt 1,3846153 = ((sin α)/(cos α))3 => 1,3846153 = (tan α)3 bzw. tan α = (1,3846153)1/3.
Mit dem Taschenrechner lässt sich daraus der Winkel bestimmen: a = 48,1º .
Um zu überprüfen, ob es sich bei dem Extremwert wirklich um das gesuchte Minimum handelt, wird die 2. Ableitung gebildet und das Ergebnis eingesetzt, das ist der 8. Schritt:
Das Ergebnis wird in die 2. Ableitung eingesetzt. Ist die 2. Ableitung an dieser Stelle größer Null, so liegt ein lokales Minimum vor. Ist die 2. Ableitung kleiner Null, so liegt an dieser Stelle ein lokales Maximum vor.
Das Bilden der 2. Ableitung kann man sich aber unter Umständen ersparen, wenn aus dem Sachzusammenhang erkennbar ist, ob es sich um ein Minimum oder Maximum handelt.
Setzt man den so errechneten Winkel in die Ausgangsgleichung l(a) = 1,8/sin α + 1,3/cos α ein, so ergibt sich l = 4,36 m. Dieses Ergebnis lässt sich am Modell auch überprüfen.
Die vorgestellte Lösungsstrategie soll nun in einer zweiten Aufgabe angewendet werden ...