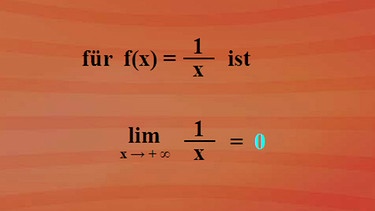Das Symbol für unendlich

Bisher konnten wir das Tangentenproblem ohne Verwendung eines Grenzwertes bewältigen. Doch bei der genauen Betrachtung von Funktionen und deren grafischer Darstellung kommen wir nicht ohne eine Grenzwertbetrachtung aus. In der Mathematik werden unendliche Werte durch eine auf der Seite liegende Acht dargestellt. Das Symbol wurde im 17. Jahrhundert für unendliche Größen eingeführt. Es ist das alte römische Zeichen für die Zahl 1000.

Die liegende Acht

Vom Omega zur liegenden Acht

Es gibt viele Deutungen, woraus diese auf der Seite liegende Acht herstammt. Eine Deutung ist, dass das Symbol für unendlich aus dem letzten Buchstaben des griechischen Alphabets, dem Kleinbuchstaben Omega, entstanden ist. Wenn man diesen Buchstaben etwas nachlässig schreibt, schließen sich die oberen Öffnungen und es entsteht das Symbol für unendlich.

Annäherung an die Null

Annäherung an die Null

Wie Sie wissen, darf man nicht durch Null teilen. Aber vielleicht geht das doch, wenn man sich der Null annähert? 5 durch 1 gibt 5. 5 geteilt durch 0,1, also ein Zehntel, ist 50. Es wird nämlich dividiert, indem man mit dem Kehrwert des Divisors multipliziert. Also 5 mal 10 Eintel. Dann 5 geteilt durch ein Hundertstel, liefert 500. Wir lassen den Nenner immer kleiner werden und das Ergebnis wird immer größer. Jetzt ist die Frage, wie lange geht das?

Der Grenzwert

Wenn der Divisor, oder bei einem Bruch der Nenner, immer näher an die Zahl Null heranreicht, also im positiven Zahlenbereich immer kleiner wird, dann wird das Ergebnis, also der Wert des Bruches, immer größer. Wir gehen davon aus, dass der Zähler oder auch Dividend eine konstante positive Zahl ist. Im Grunde genommen wird das Ergebnis unendlich groß. Diese unendliche Größe beschreiben wir durch einen Grenzwert, den Limes.

Eine nahezu nicht mehr vorhandene Maus

Der Limes für eine nahezu nicht mehr vorhandene Maus (Klicken Sie bitte auf das Bild)

Wäre die Maus unendlich klein, würde sie ewig lange an dem Käse fressen können. Mathematisch betrachtet: Wird das Stück Käse an eine Maus verteilt, deren Größe nahezu null ist, frisst sie unendlich lang. Dazu könnte man nebenstehende mathematische Schreibweise wählen. Der Limes, für Grenzwert des Bruches 'Käsestück durch Maus', ist für eine nahezu nicht mehr vorhandene Maus unendlich. Diesen Sachverhalt fassen wir nun in eine Funktion - klicken Sie bitte auf nebenstehendes Bild.

Gleich große Mäuse, die immer mehr werden

Jetzt betrachten wir noch die Umkehrung dieses Vorgangs. Wir lassen am Käsestück gleich große Mäuse fressen, aber mit immer größer werdender Anzahl.

Es können unendlich viele Mäuse werden, es wird immer ein kleinstes Stückchen für eine Maus übrig bleiben.

Array

Auch das wollen wir mit dem Grenzwert einer Funktion betrachten. Hat die Funktion f(x) den Funktionsterm 1 durch x, so ist der Grenzwert für den Term 1 durch x, wenn x gegen plus unendlich geht, gleich null.