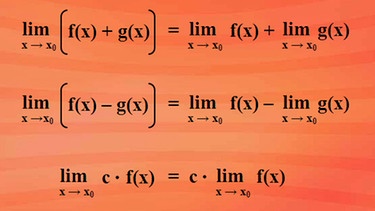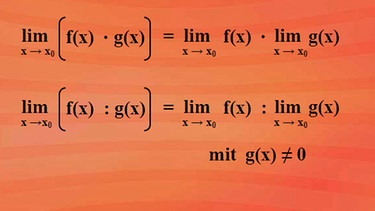Differentialrechnung Grenzwert zusammengesetzter Funktionen
Nach einer kurzen Rekapitulation des Gelernten betrachten wir noch die Grenzwertberechnung bei zusammengesetzten Funktionen. Auch das ist keine Zauberei ...
Das Wichtigste über Grenzwerte bei Funktionen kennen Sie jetzt. Folgendes sollten Sie sich merken:
Das Wichtigste über Grenzwerte bei Funktionen
- Die Bestimmung von Grenzwerten erfolgt meist über Zerlegung und Bildung von Teilgrenzwerten.
- Außer der von uns verwendeten Methode gibt es kaum weitere allgemein gültige Verfahren.
- Eine Funktion, die bei einem bestimmten x-Wert x0 nicht definiert ist, aber in der Umgebung von x0 definiert ist, besitzt an dieser Stelle eine Definitionslücke. Diese Lücke ist aber hebbar, wenn der Grenzwert für x gegen x0 existiert.
Konvergent und divergent
Mathematisch ausgedrückt, hatten die beiden in obigem Video es mit einer hebbaren Lücke zu tun. Grundsätzlich bezeichnet der renzwert, oder auch Limes genannt, denjenigen Wert einer Funktion, dem sich die Funktion in der Umgebung einer betrachteten Stelle annähert. Dieser Grenzwert existiert aber nicht in allen Fällen. Ist er existent, so sagt man, dass die Funktion konvergiert. Ist er nicht existent, dann heißt die Funktion divergent.
Grenzwerte zusammengesetzter Funktionen
Grenzwertberechnung zusammengesetzter Funktionen: Addition und Subtraktion
Sind f(x) und g(x) Funktionen, die in einer Umgebung der Stelle x0 definiert sind und für x gegen null konvergieren, so ist der Limes von f(x) plus g(x) die Summe der Grenzwerte der einzelnen Summanden - klicken Sie bitte auf nebenstehendes Bild. Gleiches gilt für die Subtraktion. Es können auch konstante Faktoren vor den Grenzwert gezogen werden.
Grenzwertberechnung zusammengesetzter Funktionen: Multiplikation und Division
Bei der Multiplikation können die Grenzwerte eines jeden Faktors bestimmt und dann multipliziert werden. Gleiches gilt für die Division, wobei natürlich der Divisor ungleich null sein muss.
Nachdem wir jetzt mit Grenzwertbestimmungen arbeiten können, ist es uns ab heute möglich, die Tangentensteigungsfunktion beziehungsweise die Ableitungsfunktion einer jeden beliebigen Funktion mit Hilfe der Bestimmung des Grenzwertes der Sekantensteigung zu ermitteln.
Allgemein gilt:
Die Funktion f(x) hat für alle x Element aus R die nebenstehende Ableitungsfunktion. Aber natürlich nur, wenn der Grenzwert auch existiert.