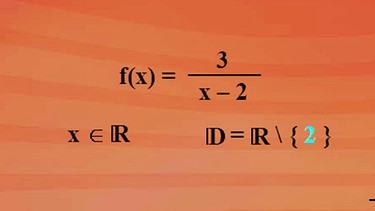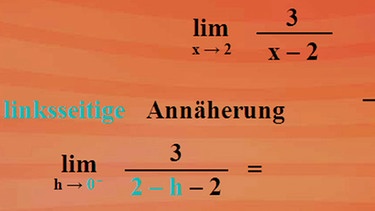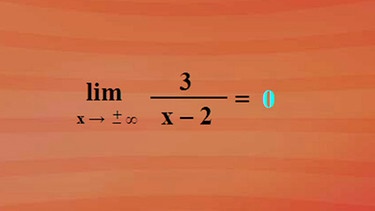Hier muss x gleich 2 in der Definitionsmenge ausgeschlossen werden (Klicken Sie bitte auf die Lupe)

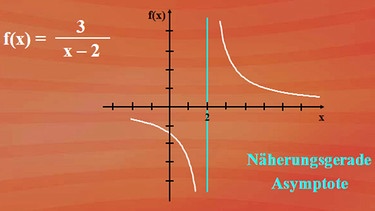
Betrachten wir die nebenstehende Funktion. In diesem Fall wird für x gleich 2 der Nenner null. Deshalb muss x gleich 2 in der Definitionsmenge ausgeschlossen werden. Für x gleich 2 gibt es also keinen Funktionswert. Aber für 2,00001 oder 1,9999 und so weiter gibt es doch einen. Es gibt also sowohl für die linksseitige als auch für die rechtsseitige Annäherung einen Grenzwert. 

Grenzwert-Berechnung mit Definitionslücke

Grenzwert-Berechnung mit Definitionslücke

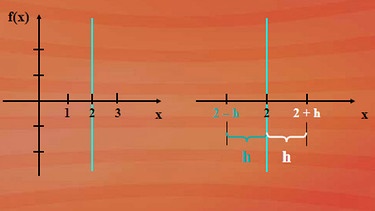
Der Fluss aus dem Video-Beispiel könnte - grafisch dargestellt - senkrecht zu unserer Definitionslücke x gleich 2 verlaufen. Der Wert x gleich 2 ist nicht möglich, es gibt für ihn keinen Funktionswert. Es handelt sich um eine Definitionslücke. Aber man kann an den x-Wert 2 sowohl von plus unendlich herkommend als auch von minus unendlich herkommend ganz nah herankommen. Wir wählen dazu den Abstand h, wobei dieser Abstand h immer kleiner werden soll.

Der Wert von h soll so klein werden, dass er nahezu null ist - wir haben also wieder eine Grenzwertrechnung, da h den Wert null ja eigentlich nicht erreicht. Normalerweise hätten wir den Grenzwert für x gegen zwei untersucht. Das geht aber nicht, weil dann im Nenner null steht. Wir behelfen uns mit einem Umweg: Wie wählen nicht 2, sondern 2 plus ein bisschen etwas, nämlich einen Wert h, den wir immer kleiner werden lassen, bis nahezu null.

Rechtsseitige Annäherung

Rechtsseitige Annäherung - klicken Sie bitte auf die Lupe.

Wegen der Definitionslücke bei x gleich 2 bestimmen wir den Grenzwert Limes für x gegen 2 von 3 durch x minus 2 - siehe nebenstehende Abbildung (klicken Sie auf die Lupe!). Wir nähern uns zuerst von rechts dem x-Wert 2. Für x setzen wir 2 plus h ein, h soll gegen null gehen. Damit erkennbar ist, dass es sich um eine rechtsseitige Annäherung handelt, schreiben wir an die Null ein hochgestelltes Pluszeichen. Die weitere Umformung entnehmen Sie der Abbildung. Das Ergebnis ist eine Konstante durch Null, also ein klarer Grenzwert, nämlich plus unendlich.

Linksseitige Annäherung

Linksseitige Annäherung - klicken Sie bitte auf die Lupe.

Bei der linksseitigen Annäherung gibt es zwei Unterschiede zur rechtsseitigen Annäherung: Wir werden den Abstandhalter h nicht addieren, sondern subtrahieren. Und zweitens werden wir statt h gegen null plus jetzt h gegen null minus für die linksseitige Annäherung schreiben. Das Ergebnis sehen Sie in nebenstehender Abbildung, klicken Sie bitte auf die Lupe.

Um den Graphen skizzieren zu können, benötigen wir noch die Grenzwerte der beiden Randwerte x gegen plus unendlich und x gegen minus unendlich. Dies lässt sich aber aufgrund der Einfachheit des Bruchterms in einer Grenzwertbestimmung bewältigen. Limes für x ist sowohl für plus unendlich als auch für minus unendlich: null. 3 durch minus unendlich ist zwar genau genommen minus null, aber minus null entspricht doch plus null.

Näherungsgerade oder Asymptote

Näherungsgerade oder Asymptote

Wir skizzieren nun den Kurvenverlauf für die Funktion. Die Stelle x gleich 2 ist nicht definiert, der Wert kann nicht erreicht werden. Es gibt für x gleich 2 eine Näherungsgerade, in mathematischer Sprache Asymptote. Bei der linksseitigen Annäherung an x gleich 2 geht der Graph gegen minus unendlich, bei der rechtsseitigen Annäherung gegen plus unendlich. Und für x gegen plus oder minus unendlich jeweils gegen null. Es gibt also noch eine zweite Näherungsgerade, die x- Achse.