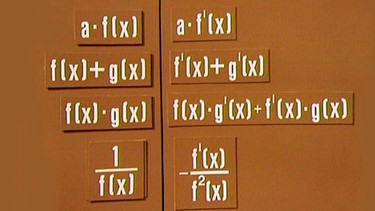Kettenregel Physikalisches Modell als Einführung
Zunächst ein Überblick über die in der vorhergehenden Lektion vorgestellten Funktionen und ihre Ableitungen sowie ein konkretes Anwendungsbeispiel.
Zu Beginn des Beitrags gibt es einen Überblick über die in der vorhergehenden Lektion vorgestellten Funktionen und ihre Ableitungen:
Funktionen und ihre Ableitungen
(a·f(x))’ = a·f’(x)
(f(x) + g(x))’ = f’(x) + g’(x)
(f(x) · g(x))’ = f(x) · g’(x) + f’(x) · g(x)
(1/f(x))’ = -f’(x)/f2(x)
Anschließend wird ein Verfahren vorgestellt, mit dem für eine Funktion Näherungswerte mit Hilfe ihrer Ableitungsfunktion ermittelt werden können.
Physikalisches Modell
Experiment zur Umsetzung der Flüssigkeitshöhe in elektrische Spannungswerte
Als erstes Anwendungsbeispiel wird ein physikalisches Modell gezeigt. Es handelt sich um einen Behälter mit parallelen Wänden und V-förmigem Querschnitt, der mit einer farbigen Flüssigkeit gefüllt ist. Die Höhe des Flüssigkeitsspiegels bzw. auch des Volumens der Flüssigkeit kann mit einem Schwimmer erfasst werden, dessen Lage über eine Schnur auf eine Rolle übertragen wird.
Umsetzung der Höheninformation in Spannungswerte durch ein Potentiometer
Die Rolle ist mit einem Potentiometer gekoppelt. Es handelt sich dabei um ein elektrisches Widerstandsbauelement, an dem mit Hilfe eines drehbaren Schleifkontakts Teilspannungen einer an den Enden angelegten Spannungen abgegriffen und einem Spannungsmessgerät (Voltmeter) zugeführt werden. Die abgegriffene, vom Voltmeter angezeigt Spannung ist somit ein Maß für die Höhe des Schwimmers.
Tabelle mit den Messergebnissen
Die Ergebnisse eines Messversuchs werden zunächst in eine Tabelle eingetragen: 0 dm => 0 Volt; 1 dm => 1 Volt; 2 dm => 4 Volt; 3 dm => 9 Volt; 4 dm => 16 Volt. Trägt man diese und viele weitere Messwerte in ein Koordinatensystem ein, deren Abszisse in dm und deren Ordinate in Volt eingeteilt ist, so zeigt sich, dass die Spannung eine quadratische Funktion der Schwimmerhöhe bzw. des Flüssigkeitsspiegels ist. (Dieses Ergebnis ist auf die besondere Bauart des Potentiometers zurückzuführen.)