Kettenregel Ermittlung von Näherungswerten
Mit HIlfe der Ableitungsfunktion finden wir nun Näherungswerte für die Funktion.
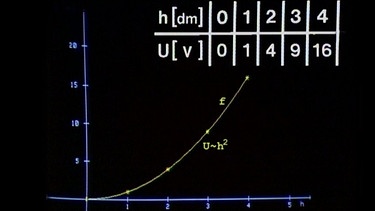
Betrachtet man nur die Zahlenwerte (die physikalischen Einheiten Volt und Dezimeter bleiben hier außer Betracht), so erhält man statt der Proportion U ~ h2 die Gleichung U = h2.
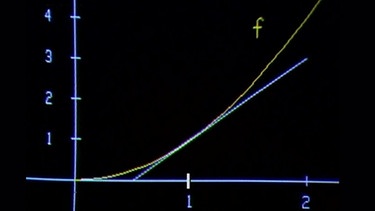
Nun sollen mit Hilfe der Ableitungsfunktion Näherungswerte für diese quadratische Funktion gefunden werden. Zunächst legt man als Beispiel an der Stelle 1 dm eine Tangente an die Kurve (Graph).
Näherungsformel
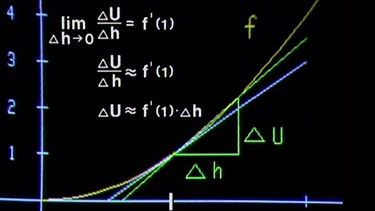
Diese Tangente ist entstanden aus einer Sekante mit der Steigung ΔU/Δh, wobei der Grenzwert ΔU/Δh (Δh gegen Null) gleich der Ableitung f’(1) ist. Durch Umstellen ergibt sich die Näherungsformel ΔU ≈ f’(1)· Δh.
Mit dieser Näherungsformel lässt sich nun eine Spannungsdifferenz ΔU als Funktion von Δh berechnen.
Berechnung der Spannungsdifferenz
Zuvor aber wird diese Spannungsdifferenz mit einem Experiment bestimmt. Dazu wird in den Behälter soviel Flüssigkeit gegossen, dass der Spiegel von 1 dm auf 1,5 dm Höhe steigt. Zugleich wird am Voltmeter der Anstieg der Spannung, also die Spannungsdifferenz, gemessen. Für eine Höhendifferenz Δh = 0,5 dm ergibt sich eine Spannungsdifferenz ΔU = 1,25 V.
Die Berechnung von ΔU mit der Formel ΔU ≈ f’(1)· Δh ergibt dagegen ΔU ≈ 2·0,5 V = 1 V. Das ist zwar nicht der genaue Messwert, aber schon ein guter Näherungswert.
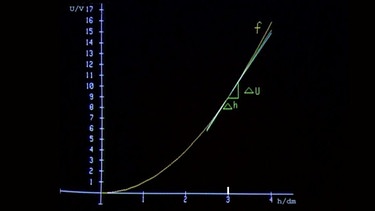
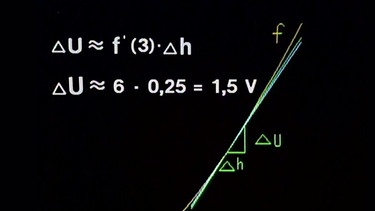
In einem zweiten Rechenexperiment legen wir die Tangente an den Graphen bei der Höhe h = 3 dm.
Für eine gewählte Höhendifferenz Δh = 0,25 dm wird nach der Formel ΔU ≈ f’(3)· Δh die Spannungsdifferenz ΔU berechnet. Es ergibt sich ΔU ≈ 6 · 0,25 V = 1,5 V. (Wegen (x2)’ = 2x).