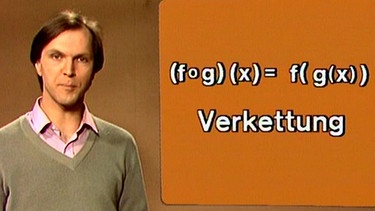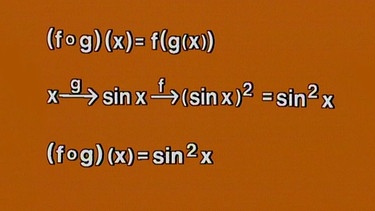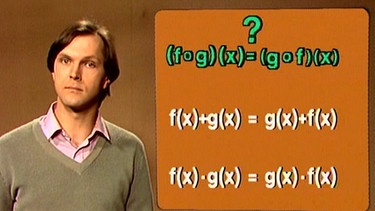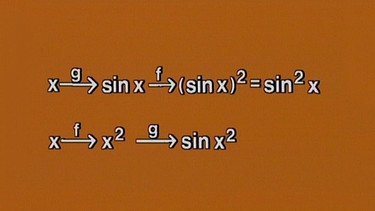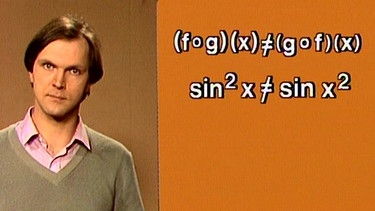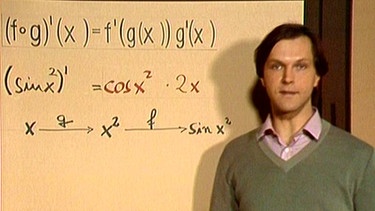Verknüpfung von Funktionen zu einer "verketteten Funktion"

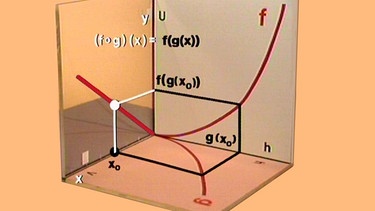
Bezeichnet man die Achsen des Koordinatensystems dieser linearen Funktion mit x und y, so wird z.B. der  Funktionswert y(x₀) von der Teilfunktion g(x₀) und diese von der Teilfunktion f(x₀) bestimmt, insgesamt also von der Funktion f(g(x₀)). Diese Kombination f(g(x₀)) von zwei hintereinander ausgeführten Funktionen wird auch (f ◦ g)(x), gesprochen "f verknüpft mit g von x" (das Symbol ◦ ist ein Verknüpfungszeichen), geschrieben.

Die verkettete Funktion

Die verkettete Funktion

Diese Verknüpfung von zwei hintereinander auszuführenden Funktionen wird als Verkettung bezeichnet. Die zuerst auszuführende Funktion, hier also g(x), wird als "innere Funktion", die danach auszuführende Funktion, also f(x), als "äußere Funktion" bezeichnet.

Beispiel einer verketteten Funktion

sin Quadrat x als Verkettung der Sinusfunktion und der Quadrierfunktion

Als rein mathematisches Beispiel einer verketteten Funktion wird (f ◦ g)(x) = sin2x betrachtet. Zunächst wird die Funktion g(x) = sin x ausgeführt, auf diese wird dann die Funktion f(g(x))² angewendet. Die innere Funktion ist hier die Sinusfunktion, die äußere die Quadrierfunktion.

Vertauschen verketteter Funktionen

Lassen sich die verketteten Funktionen vertauschen?

Dieser Typ der verketteten Funktion soll nun auf seine Eigenschaften untersucht werden. Lassen sich vielleicht – wie bei der Addition oder der Multiplikation von Funktionen – die beiden Funktionen vertauschen?

Ist sin Quadrat x gleich sin x Quadrat?

Als Beispiel werden die beiden Funktionen der Verkettung (f ◦ g)(x) = sin2x vertauscht, also es wird x zunächst quadriert und dann der Sinus gebildet.

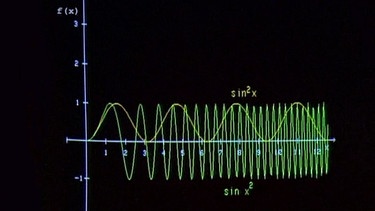
Vergleich der Verkettungen

sin Quadrat x und sin x Quadrat sind völlig unterschiedliche Funktionen

Der Vergleich der beiden Verkettungen am Computerbildschirm zeigt, dass es sich um völlig verschiedene Funktionen handelt.

Die Verkettung von Funktionen ist nicht kommutativ

Die Verkettung von Funktionen ist also nicht kommutativ, d.h. in unserem Beispiel sin²x ≠  sin x².

Kettenregel

Die Kettenregel zur Ableitung von verketteten Funktionen

Wie aber werden verkettete Funktionen differenziert? Die Ableitung der verketteten Funktion (f ◦ g)(x₀), also (f ◦ g)’(x₀), lautet f’(g(x₀))· g’(x₀). D.h., zwei verkettete Funktionen werden abgeleitet, indem man die Ableitung der äußeren Funktion mit der Ableitung der inneren Funktion multipliziert.

So wird die Ableitung von sin x Quadrat berechnet

So lässt sich dann auch die oben angegebene Aufgabe lösen, die Ableitung von sin x², also (sin x²)’ zu berechnen. Man differenziert zunächst die äußere Funktion zu cos x² und dann die innere Funktion zu 2x . Also (sin x²)’ = cos x² · 2x.