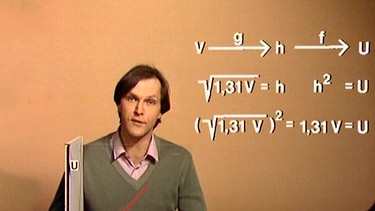Abhängigkeit des Flüssigkeitsspiegels vom Volumen

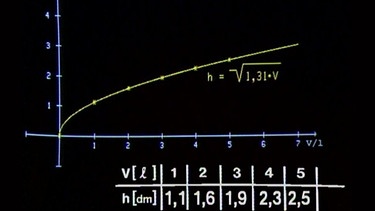
Im Folgenden wird nun untersucht, welcher Zusammenhang bei dieser speziellen Form eines Gefäßes zwischen dem Wasserstand und dem Volumen besteht. Dazu werden fünfmal je 1 Liter Wasser in das Gefäß gegossen und jeweils der Flüssigkeitsstand abgelesen. Die Abbildung zeigt, dass der Flüssigkeitsstand nicht direkt proportional zum Volumen steigt.

h = f(V) ist eine Wurzelfunktion

Trägt man die ermittelten Werte in ein Koordinatensystem ein, so lässt sich leicht erkennen, dass es sich um eine Wurzelfunktion handelt. Eine genaue geometrische Untersuchung des Behälters ergibt für die Zahlenwerte die Funktionsgleichung
h = (1,31 · V)^0,5.

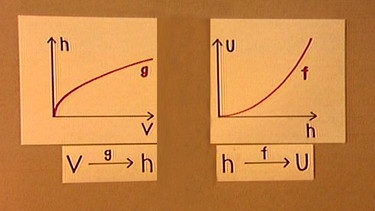
Gegenüberstellung der beiden Funktionen

Gegenüberstellung der beiden Funktionen h = g(V) und U = f(h)

Nun werden die beiden Zuordnungen h = g(V), also die Wurzelfunktion, und U = f(h), also die quadratische Funktion, einander gegenübergestellt.

Gegenüberstellung der beiden Funktionen

Setzt man die Diagramme der Funktionen h = g(V) und U = f(h) im rechten Winkel zusammen und überträgt die Werte der Funktion h = g(V) in das Koordinatensystem der Funktion U = f(h), so erhält man eine neue Funktion U = h(V) und die Werte dieser Funktion ergeben eine Gerade. Auch durch eine einfache Rechnung lässt sich dieses Ergebnis erklären: Setzt man für h die Funktion (1,31 · V)^0,5 in die Funktion h² = U ein, so ergibt sich ((1,31 · V)^0,5)² = U bzw. U = 1,31·V, also eine lineare Funktion.