Kurvendiskussion 1 Genauere Analyse
Wir wollen nun eine genauere Analyse durchführen.
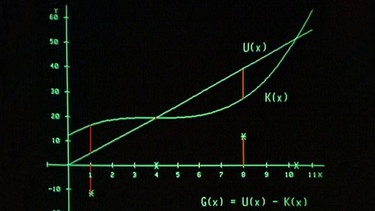
Für eine genauere Analyse wird ein PC benutzt, auf dessen Bildschirm zunächst die Graphen der Funktionen U(x) und K(x) dargestellt werden. Für ausgewählte Werte von x, x = 1 und x = 8, werden die Differenz zwischen den Funktionen ermittelt und die zugehörigen Punkte in dem Diagramm dargestellt.
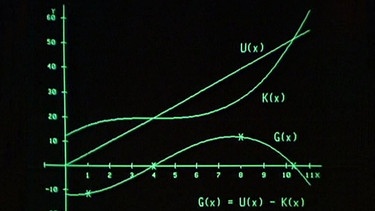
Zeichnet man die Punkte für alle x-Werte im Definitionsbereich, so ergibt sich der Graph der Funktion G(x) = U(x) – K(x) .
Der Teil des Graphen, in dem die Funktion monoton steigt, lässt sich grob durch Anlegen einer Tangente bestimmen. In dem Bereich, in dem der Winkel α zwischen der Tangente und der x-Achse zwischen 0 und 90° beträgt, steigt die Kurve. In diesem Bereich ist auch die Steigung der Tangente, d.h. die Ableitung der Funktion, positiv. In dem Bereich, wo die Steigung der Tangente, d.h. auch die Ableitung der Funktion, negativ ist, fällt die Funktion.
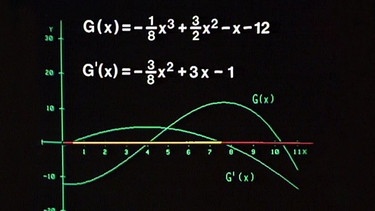
Um den Bereich, in dem die Funktion G(x) monoton steigt, genau zu erfassen, bildet man die Ableitung G’(x) = -(3/8)x2 + 3x –1 . Wie die Abbildung zeigt, ist ihr Graph eine nach unten weit geöffnete Parabel. Der Bereich zwischen den beiden Schnittpunkten, also den Nullstellen, ist gelb markiert, hier ist die Ableitungsfunktion positiv, die Funktion G(x) also monoton steigend. Vor und nach den Nullstellen, also in den rot markierten Bereichen, ist die Funktion G(x) fallend.