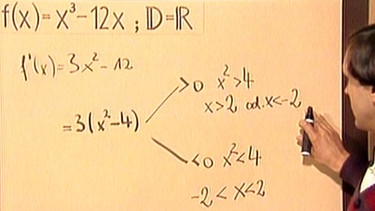Kurvendiskussion 1 Monoton steigende oder fallende Funktion
Man kann die Bereiche, in denen eine Funktion monoton steigend oder fallend ist, auch ohne Zeichnung oder Computer berechnen.
Funktion, Ableitungsfunktion und die positiven bzw. negativen Bereiche der Ableitungsfunktion
Als Beispiel dient die Funktion f(x) = x3 – 12x . Ihre Ableitungsfunktion lautet f ’(x) = 3x2 – 12 .
Sucht man die Nullstellen, also 3x2 – 12 = 0 bzw. 3(x2 – 4) = 0, so erhält man für f’ > 0 die Lösung x2 > 4 bzw. x > 2 bzw. x < -2. Demnach ist für –2 < x < 2 die Ableitungsfunktion f ’(x) negativ, d.h. f(x) ist in diesem Bereich fallend.
Bereiche der steigenden bzw. fallenden Funktion
Lässt man den Graphen der Funktion f(x) = x3 – 12x am Computerbildschirm anzeigen, so bestätigt sich das Ergebnis der obigen Rechnung.
Zusammenfassung:
Ist eine Funktion f(x) in einem Intervall I differenzierbar, so gilt: In den Bereichen, in denen ihre Ableitungsfunktion Funktion f ’(x) positiv ist, also f ’(x) > 0, ist f(x) monoton steigend. In den Bereichen, in denen ihre Ableitungsfunktion Funktion f ’(x) negativ ist, also f ’(x) < 0, ist f(x) monoton fallend.