In der Mathematik spricht man nicht gerne über eine Kurve, wenn man sie nicht mathematisch beschreiben kann. Sozusagen ist in der Mathematik eine Kurve die grafische Darstellung eines funktionalen Zusammenhangs. Und liefert dieser funktionale Zusammenhang eine Gerade, dann ist eben die Gerade sozusagen die Kurve der Funktion. Diese spezielle Funktion ändert aber ihr Verhalten nie. Und ihr Graph ändert demnach seine Steigung nicht.

Grafische Darstellung der linearen Funktion

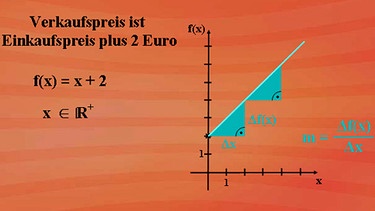
Ein Beispiel: Der Chef ermittelt den Verkaufspreis in Abhängigkeit vom Einkaufspreis. Er schlägt immer zwei Euro auf: Verkaufspreis ist Einkaufspreis plus zwei Euro. Es ergibt sich eine lineare Funktion, die grafisch dargestellt aufgrund der eingeschränkten Definitionsmenge R+ den Verlauf einer Halbgeraden hat.

Rekapitulation: Steigung einer Geraden

Wissen Sie noch, wie die Steigung einer Geraden bestimmt wird? Der Steigungsfaktor m war der Quotient aus einer bestimmten Wegstrecke in x- Achsenrichtung und der daraus resultierenden Wegstrecke in f(x)- Achsenrichtung.

Der Steigungsfaktor

Die Wegstrecke in x-Achsenrichtung, mit Delta x bezeichnet, bildet den Nenner und die f(x)-Achsenrichtung Delta f(x) den Zähler des Steigungsfaktors m. Es ist egal, an welcher Stelle des Graphen der linearen Funktion Sie das Steigungsdreieck ansetzen, es liefert stets den gleichen Steigungsfaktor.