Differentialrechnung Die Steigung einer Funktion
Wie berechnet man die Steigung eines Funktionsgraphen, der nicht geradlinig verläuft? Das zeigen wir am praktischen Beispiel eines Zeit-Weg-Diagramms:
Anders als bei der Steigung einer Geraden ist es bei Funktionsgraphen, die nicht geradlinig verlaufen - zum Beispiel bei einem Zeit-Weg-Diagramm für eine Bewegung mit konstanter Beschleunigung.
Das Zeit-Weg-Diagramm
Das Auto im Beispiel bewegt sich gleichmäßig beschleunigt auf ebener Strecke. Die Wegstrecke wird in Abhängigkeit von der Zeit gemessen und in ein Koordinatensystem übertragen. Es ergibt sich ein Parabelbogen.
Steigung und Veränderung
Für diesen Parabelbogen lässt sich die Steigung nicht mehr so einfach angeben: Der Graph verändert ständig sein Verhalten - er steigt ständig, hat aber an jedem Zeitpunkt t eine andere Steigung.
Das Änderungsverhalten einer Funktion lässt sich also am Graphen dieser Funktion ablesen. Die Funktionswerte ändern sich stark, wenn der Funktionsgraph steil ansteigt oder fällt. Man spricht von der Steigung des Graphen.
Berechnung der mittleren Steigung
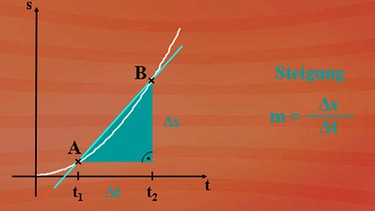
Die mittlere Steigung, vergleichbar mit der globalen Veränderung, lässt sich leicht berechnen: Man wählt ein Intervall zwischen zwei Punkten (in nebenstehender Grafik: A und B) und ersetzt den wirklichen Kurvenverlauf durch eine Gerade. Wie im vorherigen Beispiel bilden wir wieder ein Steigungsdreieck und bestimmen die Steigung m, wie wir es von linearen Funktionen gewöhnt sind. Obwohl der tatsächliche Funktionsgraph in jedem Punkt eine andere Steigung besitzt, ist es möglich, für ein bestimmtes Intervall einen Mittelwert zu bilden.
Sekantensteigung

Sekantensteigung
Die eingezeichnete Gerade schneidet den Funktionsgraphen in den Punkten A und B und ist deshalb eine Sekante des Funktionsgraphen. Die Sekantensteigung m ist auf das Intervall von a bis b bezogen und lässt sich gemäß nebenstehender Formel berechnen.
Beschreibung des Änderungsverhaltens
Man kann das Änderungsverhalten einer Funktion auf zweierlei Weise beschreiben:
- global durch eine mittlere Änderung
- lokal durch eine momentane Änderung - bei einem Funktionsgraphen bedeutet dies:
- für das globale Änderungsverhalten: die mittlere Steigung über einem gewissen Intervall
- für das lokale Änderungsverhalten: die Steigung in einem Punkt
Sekante und Tangente
Unter der Sekante eines Graphen versteht man eine Gerade, die den Graphen in zwei Punkten schneidet. Lässt man diese beiden Punkte immer enger aneinander rücken, so wird das verwendete Intervall immer kleiner - solange, bis von dem Intervall nichts mehr vorhanden ist. Dann fallen die Punkte A und B sozusagen zusammen. Der Graph hat dann keine zwei Schnittpunkte einer Sekante, sondern nur noch einen Berührpunkt. Und die Gerade, welche den Graphen dann in diesem Punkt berührt, heißt Tangente. Sie hat die Steigung, welche der Funktionsgraph in diesem Punkt besitzt.