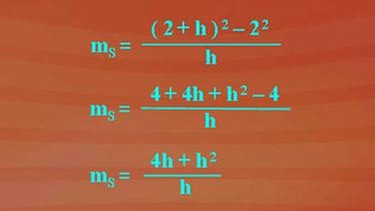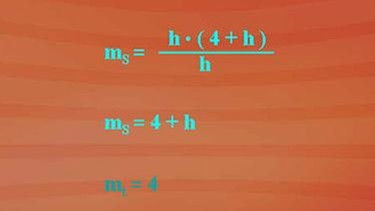Die Berechnung der Tangentensteigung spielen wir jetzt am Beispiel einer Normalparabel durch:

Steigung der Tangente am Beispiel einer Normalparabel (Klicken Sie bitte auf die Lupe.)

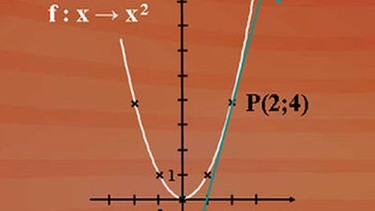
Zur Erinnerung: Eine Parabel hat in jedem Punkt des Graphen eine andere Steigung. Uns interessiert die Steigung im Punkt 2 und 4 (siehe nebenstehende Abbildung).

Berechnung der Steigung: Klicken Sie bitte auf die Lupe

Sie ist dann auch die Steigung der Tangente an die Parabel in diesem Punkt.

Berechnung der Steigung

Wie der Differenzenquotient des Steigungsfaktors für einen benachbarten Punkt berechnet wird, sehen Sie nachfolgend:

Weiteres Beispiel

Berechnung der Steigung - klicken Sie bitte auf die Lupe

Wir haben gesehen, dass die Steigung in einem Punkt P des Graphen nur vom x- Wert des betreffenden Punktes abhängig ist. Es war das Doppelte der x-Koordinate. Berechnen wir es nun für den Punkt P mit den Koordinaten 3 und 9: Wir setzen 3 für x, demnach 9 für x hoch zwei. Die Sekantensteigung und die weitere Umformung zeigt die nebenstehende Abbildung. Die Tangentensteigung für h gleich Null hat den Wert 6 - wieder das Doppelte des x-Wertes des betreffenden Punktes.

Die Tangentensteigungsgleichung

Wir können folgern, dass jeder Punkt der Parabel mit Zuordnungsvorschrift x gegen x hoch zwei die Steigung 2 mal x besitzt.

Tangentensteigungsgleichung - klicken Sie bitte auf die Lupe

Als Tangentensteigungsfaktor wählen wir das Symbol f'. Wie die Funktion f(x) die Tangentensteigungsgleichung liefert, sehen Sie bei Klick auf nebenstehendes Bild. Die Tangentensteigungsfunktion wird auch als Ableitungsfunktion bezeichnet.

Die Lösung des Tangentenproblems

Die Funktionsgleichung f(x) = x³ hat die Tangentensteigungsfunktion, kurz Ableitungsfunktion, f'(x) = 3 mal x².

Das Tangentenproblem scheint gelöst zu sein. Die Tangentensteigung ist der Grenzwert der Sekantensteigungsfunktion, sofern dieser existiert. Und die Grenzwertsätze für Funktionen haben wir bisher noch nicht benötigt.