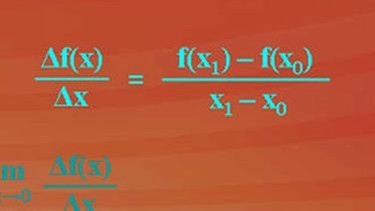Der Differentialquotient

Die Aufgabe, die Tangente an die Bildkurve einer Funktion f(x) zu einem bestimmten Punkt P mit den Koordinaten x und f(x) zu legen, führt bei der Ermittlung der Steigung zu einem Quotienten besonderer Art, dem Differentialquotienten. Die Untersuchung der Eigenschaften des Differentialquotienten einer Funktion ist Gegenstand der Differentialrechnung. Als Voraussetzung dafür muss man wissen, wie man den Steigungsfaktor einer Geraden bildet.

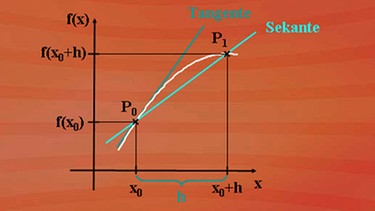
Der Graph der Funktion f verläuft zwischen den Punkten P₀ und P₁ verschieden steil. Man kann über die Steilheit des Graphen an einer bestimmten Stelle x* zwischen x0 und x1 keine genaue Angabe machen. Es lässt sich lediglich eine mittlere Steilheit zwischen P₀ und P₁ angeben, die der Steigung der Geraden g durch P₀ und P₁ entspricht. Der Graph wird sozusagen zwischen den Punkten P₀ und P₁ durch die Gerade linearisiert.

Der Differenzenquotient

Funktionsterm der Geraden

Den Funktionsterm der Geraden sehen Sie in nebenstehender Abbildung. Der Steigungsfaktor wird aus den Koordinatenwerten der beiden Punkte P₀ und P₁ ermittelt. Da er ein Quotient aus zwei Differenzen ist, heißt er Differenzenquotient.

Je näher der Punkt P₁ an den Punkt P₀ heranrückt, desto kleiner werden die Werte im Zähler und Nenner des Differenzenquotienten. Wenn P₁ in P₀ liegt, ist der Quotient null durch null. Geometrisch ist uns klar, dass es eine Gerade gibt, die den Graphen der Funktion im Punkt P₀ berührt, also eine Tangente. Bei der Bestimmung der Steigung treffen wir aber auf erhebliche Schwierigkeiten - es ist nämlich nicht erlaubt, durch null zu teilen.

Aus Sekante wird Tangente

Die Sekante wird zur Tangente

Zusammenfassend lässt sich sagen: Wir suchen die Steigung des Funktionsgraphen im Punkt P₀. Dazu lassen wir den Summanden h immer kleiner werden, bis aus der Sekante eine Tangente wird. Der Wert von h bestimmt die Lage des Punktes P₁. Für h gleich null fallen P₁ und P₀ zusammen - was ja unser Ziel ist.

Der Limes

Differenzenquotient - klicken Sie bitte auf die Lupe

Wenn wir aber nicht durch null teilen dürfen, müssen wir zumindest versuchen, so nahe wie möglich an den Nennerwert null herangehen zu können - das heißt, wir müssen den Summanden h möglichst klein werden lassen. Er soll also gegen null gehen, aber null gerade nicht erreichen. Im Differentialquotient geht dann der Wert für delta x gegen null. Wir suchen einen Grenzwert und nennen ihn "Limes" - lateinisch für "Grenze".

Differenzenquotient und Differentialquotient

Differenzenquotient - Klicken Sie bitte auf die Lupe

In nebenstehendem Bild sehen Sie den Differenzenquotienten - klicken Sie bitte auf die Lupe. Bildet man von ihm den Grenzwert, also Limes für delta x gegen null, heißt dieser Ausdruck Differentialquotient. Wie sich aus ihm die Tangentensteigung berechnen lässt, sehen Sie, wenn Sie die Grafik anklicken. h  geht gegen null. Zusammengefasst bleibt im Nenner nur h stehen.