Grundkurs Mathematik (13) 13.3. Kathete und Ankathete
Im nächsten Schritt wollen wir die Winkelmaßberechnung auf beliebige rechtwinklige Dreiecke übertragen. Dazu differenzieren wir die beiden Katheten in Kathete und Ankathete.
Die y-Koordinate des Punktes P ist nichts anderes als r mal Sinus alpha. Die Länge dieser Strecke ist aber - wie eben berechnet - 3,816 Meter.
Bei einem Radius gleich vier Meter ergibt sich somit vier Meter mal Sinus alpha ist gleich 3,816 Meter. Durch vier Meter geteilt erhalten wir Sinus alpha gleich 3,816 durch vier, oder 0,954. Mit dem Taschenrechner berechnet ein Winkelmaß von 72,5 Grad.
Das gleiche Winkelmaß haben wir über die Berechnung mit Kosinus alpha erhalten. Es scheint also korrekt zu sein.
Vielleicht ist es uns möglich, dies auf beliebige rechtwinklige Dreiecke übertragen zu können. Dazu nochmals unser Koordinatensystem.
Differenzierung der beiden Katheten
Die Ankathede und Gegenkathede: Bitte klicken Sie auf die Lupe.
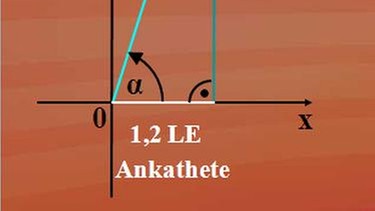
Die x-Koordinate und die y-Koordinate des Punktes P bilden mit der Strecke OP ein rechtwinkliges Dreieck mit der Hypotenuse OP und den beiden Katheten xP und yP. Um die zwei Katheten voneinander begrifflich unterscheiden zu können, bezeichnet man die Kathete, die dem maßgebenden Winkel anliegt, - also hier xP - als Ankathete und die dem maßgebenden Winkel gegenüberliegende Kathete - hier yP - als Gegenkathete.
Hätten wir als maßgebenden Winkel den Winkel bei P gewählt, hätte sich Ankathete und Gegenkathete gegenseitig vertauscht. Sie müssen also die beiden Katheten immer von dem der Berechnung zugrundeliegenden Winkel aus betrachten.
Aufgepasst!:
Die diesem Winkel anliegende Kathete heißt Ankathete und die diesem Winkel gegenüberliegende Kathete Gegenkathete.
Für die Hypotenuse ist es eindeutig, denn dies ist immer die Seite, die dem rechten Winkel gegenüberliegt. In der Verwechslung liegt die größte Fehlerquelle bei Berechnungen mit Winkelfunktionen im rechtwinkligen Dreieck.
Berechnungsbeispiel
Beziehung der Winkel und Seiten im rechtwinkligen Dreieck: Bitte klicken Sie auf die Lupe.
Unsere Hypotenuse betrug vier Längeneinheiten (speziell Meter), die Ankathete 1,2 Längeneinheiten und die Gegenkathete 3,816 Längeneinheiten. Unsere Berechnungen ergaben über Kosinus alpha, Kosinus alpha gleich 1,2 geteilt durch vier und über Sinus alpha, Sinus alpha gleich 3,816 durch vier.
Schreiben wir statt 1,2 allgemein Ankathete, statt 3,816 Gegenkathete und statt vier Hypotenuse haben wir allgemeine Beziehungen zwischen Seiten und Winkeln im rechtwinkligen Dreieck.