Grundkurs Mathematik (13) Tangens-Berechnung mittels Katheten
Der Tangens eines Winkels kann auch in einem beliebigen rechtwinkligen Dreieck eingesetzt werden, man muss nur richtig einsetzen und die Gleichung umformen ... Das rechtwinklige Dreieck muss nicht im Koordinatensystem liegen. Es kann ganz beliebig sein.
Zum Beispiel könnte in einem Dreieck ABC der rechte Winkel am Eckpunkt C auftreten. Dann ist die dem Eckpunkt C gegenüberliegende Seite die Hypotenuse, und die beiden anderen Dreiecksseiten sind die Katheten, von denen dann noch zu überprüfen ist, welche Seite Ankathete und welche Seite Gegenkathete ist.
Für den Winkel alpha gilt dann::
- Sinus alpha ist Länge der Gegenkathete des Winkels alpha durch Länge der Hypotenuse.
- Kosinus alpha ist Länge der Ankathete des Winkels alpha durch Länge der Hypotenuse.
Für den Winkel beta gilt dann:
- Sinus beta ist Länge der Gegenkathete des Winkels beta durch Länge der Hypotenuse.
- Kosinus beta ist Länge der Ankathete des Winkels beta durch Länge der Hypotenus
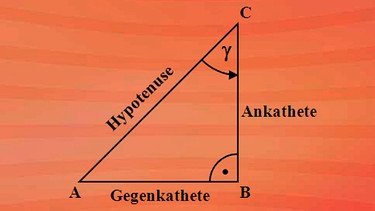
Befindet sich der rechte Winkel am Eckpunkt B, ändern sich dementsprechend die Beziehungen. Jetzt ist die Strecke AC Hypotenuse und vom Winkel gamma aus betrachtet AB die Gegenkathete und BC die Ankathete.
Einsatz des Tangens
Gibt es nun auch eine Möglichkeit, den Tangens eines Winkels im rechtwinkligen Dreieck einzusetzen?
Zu Beginn dieser Folge haben wir einen Zusammenhang zwischen Sinus, Kosinus und Tangens verwendet. Es hatte mit der Steigung einer Geraden zu tun. Tangens alpha war gleich Sinus alpha durch Kosinus alpha. Setzen wir für Sinus alpha und Kosinus alpha die Quotienten Länge der Gegenkathete durch Hypotenuse und Länge der Ankathete durch Hypotenuse, ergibt sich ein Doppelbruch.
Für das Rechnen mit Brüchen gilt: Brüche werden dividiert, indem man mit dem Kehrwert des Divisors multipliziert. Somit ergibt sich für unseren Doppelbruch ein einfacher Bruch.
Klicken Sie bitte auf die Lupe
Tangens alpha ist im Zähler: Länge der Gegenkathete mal Hypotenuse. Im Nenner steht: Hypotenuse mal Länge der Ankathete. Der im Zähler und Nenner auftretende Faktor Hypotenuse kann gekürzt werden und es ergibt sich für den Tangens eines Winkels im rechtwinkligen Dreieck:
Tangens alpha ist der Quotient aus Länge der Gegenkathete durch Länge der Ankathete.