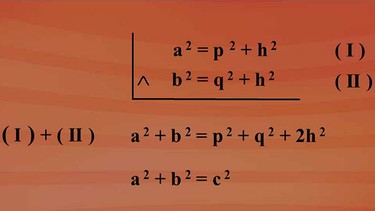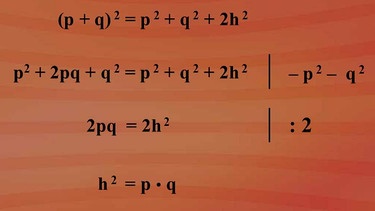11. Sätze am rechtwinkligen Dreieck 11.3. Dreieckshöhe / Hypotenusenabschnitte
Das rechtwinklige Dreieck liefert besondere Zusammenhänge - zum Beispiel einen Zusammenhang zwischen der Dreieckshöhe und den beiden Hypotenusenabschnitten - eine praktische Anwendung des Lehrsatzes von Pythagoras.
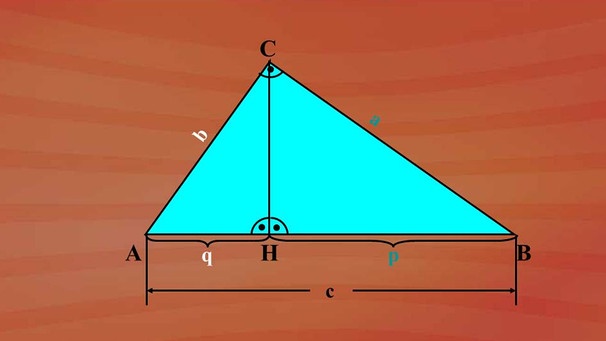
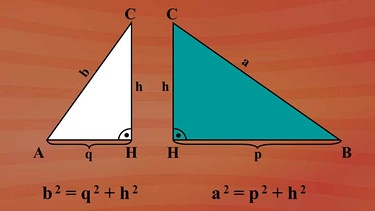
Betrachten wir noch mal das rechtwinklige Dreieck ABC mit der Höhe h und den Hypotenusenabschnitten p und q. Die Höhe teilt das Dreieck in zwei Teildreiecke, die am Höhenfußpunkt H wiederum rechtwinklig sind.
Anwendung des Lehrsatzes von Pythagoras
Wir trennen die Teilbereiche voneinander, damit man sie besser betrachten kann: Es sind zwei rechtwinklige Dreiecke, bei denen wir dank Pythagoras eine Beziehung zwischen den Dreiecksseiten kennen.
Im Dreieck AHC gilt:
die dem rechten Winkel gegenüberliegende Seite b2 = die Summe aus den Quadraten der Kathetenlängen q und h, also q2 + h2 .
Im Dreieck HBC ergibt sich:
"a2 = p2 + h2 ".
Zusammenfassung zu einem Gleichungssystem
Klicken Sie bitte auf die Lupe
Da beide Gleichungen im Grunde genommen aus einem Dreieck ABC stammen, kann man sie in einem Gleichungssystem zusammenfassen. Und Gleichungen eines Systems dürfen nach dem Additionsverfahren zusammengezählt werden. Den weiteren Rechenweg sehen Sie in nebenstehender Grafik - klicken Sie bitte auf die Lupe.
Jetzt haben wir eine Gleichung, in der fast alle Strecken, die wir in unserem Dreieck eingezeichnet haben, enthalten sind.
Eliminieren der Seitenlängen
Klicken Sie bitte auf die Lupe
Wir wollten aber eine Beziehung zwischen der Höhe h und den Hypotenusenabschnitten p und q. Also gehen wir auf die Suche, wie wir die Seitenlängen a und b eliminieren können. Und da muss uns einfallen, dass im Dreieck ABC die Beziehung "c2 = a2 + b2 " gilt. Diese Gleichung wenden wir an - siehe nebenstehende Grafik. Schließlich erhalten wir eine Gleichung, in der nur noch die gewünschten Streckenlängen vorkommen.
Vereinfachung der Gleichung
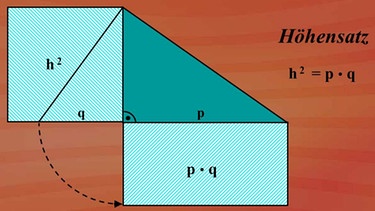
Diese Gleichung werden wir jetzt nach den Regeln der Algebra weit möglichst vereinfachen. Als erstes bringen wir die binomische Formel in die Summenschreibweise und erkennen, dass p2 und q2 auf beiden Gleichungsseiten auftaucht. Den weiteren Rechenweg sehen Sie in nebenstehender Grafik - klicken Sie bitte auf die Lupe. Das Ergebnis: h2 = p · q. Diesen Zusammenhang bezeichnet man als Höhensatz im rechtwinkligen Dreieck - der Höhensatz des Euklid.
Der Höhensatz des Euklid:
Im rechtwinkligen Dreieck ist das Quadrat über der Höhe auf der Hypotenuse flächengleich mit dem Rechteck aus den Längen der Hypotenusenabschnitte. Kurz:
h2 = p · q.