12. Sinus-, Kosinus- und Tangensfunktion 12.2. Polarkoordinaten
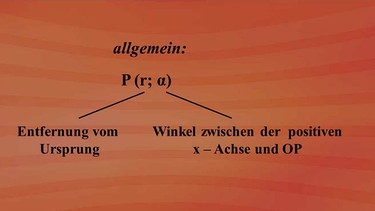
Jeder Punkt kann im Koordinatensystem auch durch die Angabe von r und alpha gekennzeichnet werden. r ist die Entfernung vom Koordinatenursprung und alpha der Winkel zwischen der positiven x-Achse und OP.
Somit kennen wir zwei Möglichkeiten für die Auffindung von Punkten im Koordinatensystem. Zum einen die altbekannten kartesischen Koordinaten mit x und y, zum andern die neuen Polarkoordinaten mit r und alpha.
Kartesischen Koordinaten / Polarkoordinaten
Wie kann man aus den Polarkoordinaten die kartesischen und umgekehrt aus den kartesischen Koordinaten die Polarkoordinaten ermitteln?
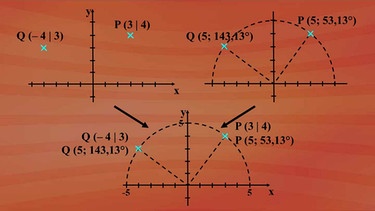
Klicken Sie bitte auf nebenstehende Grafik und betrachten Sie noch einmal die beiden Systeme unseres Beispiels. Zuerst die kartesischen Koordinaten, dann die Polarkoordinaten. Ein Übereinanderklappen der beiden Systeme zeigt, dass es sich um identische Punkte P und Q handelt, die auf unterschiedliche Art und Weise ihren festgelegten Platz finden.
Ein praktisches Beispiel
Auf unserer Europaflagge lassen sich die Sternchen über die Polarkoordinaten leicht bestimmen, da sie auf einem Kreisbogen in gleichen Abständen angeordnet sind. Bei zwölf Sternchen müssen das Sektoren mit 360 Grad für den Vollkreis geteilt durch zwölf, also 30 Grad sein.
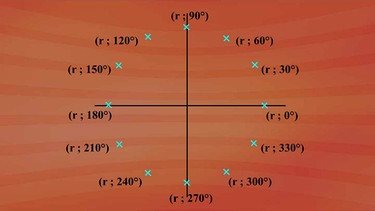
Egal bei welchem fest gewählten Radius r, die Sternchen liegen gleich verteilt in einem Koordinatensystem mit den Polarkoordinaten r und 0 Grad, r und 30 Grad, r und 60 Grad, r und 90 Grad und so weiter bis r und 330 Grad.
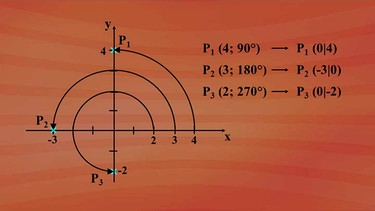
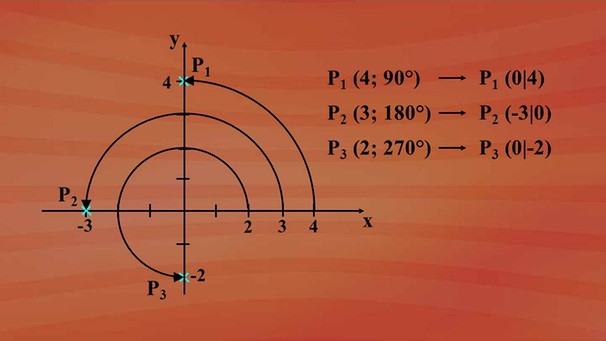
Wie kann man daraus auf die kartesischen Koordinaten kommen? Für Punkte auf den Koordinatenachsen ist es nicht schwer: Wählen wir die Polarkoordinaten mit Radius r = 4 und Winkel α = 90 Grad. Es ergibt sich ein Punkt auf der y-Achse mit den kartesischen Koordinaten 0 und 4.
Für Radius r = drei und Winkel α = 180° finden wir den Punkt P auf der x-Achse mit den Koordinatenwerten -3 und 0.
Für r = 2 und α =270° lauten die kartesischen Koordinaten des Punktes P3 (0 und -2).
Ein weiteres Beispiel
Bei den Punkten P und Q aus unserem Anfangsbeispiel ist die Ermittlung der kartesischen Koordinaten aus den Polarkoordinaten nicht so einfach. Schauen wir uns dazu noch einmal den Punkt P an.
Er hatte den Abstand fünf Längeneinheiten vom Koordinatenursprung und die Gerade OP bildete mit der positiven x-Achse den Winkel 53,13 Grad.
Der Schnittpunkt des zweiten Schenkels des angetragenen Winkels 53,13 Grad mit dem Kreisbogen um den Nullpunkt mit Radius fünf Längeneinheiten liefert die genaue Lage des Punktes P.
Aus der Zeichnung kann abgelesen werden - wenn sauber gezeichnet wurde - dass der Punkt P die kartesischen Koordinaten 3 und 4 hat.
Veränderter Winkel alpha
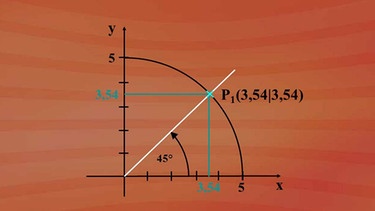
Verändern wir nun den Winkel alpha in unserer Zeichnung und lassen den Radius von fünf Längeneinheiten fest, kann man erkennen, dass sich die kartesischen Koordinaten in Abhängigkeit des Winkels alpha ändern. Zum Beispiel bei α = 45 Grad.
Wenn man ganz genau zeichnet, erhält man die kartesischen Koordinaten 3,54 und 3,54. Dass x- und y-Koordinaten den gleichen Wert haben, ist erklärbar, da die Gerade OP bei α = 45 Grad die Winkelhalbierende des ersten und dritten Quadranten bildet.
Fazit:
Eine Änderung des gewählten Radius hat eine entsprechende Änderung der kartesischen Koordinaten zur Folge.
Verdoppelter Kreisradius
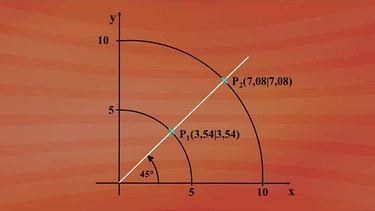
Was geschieht mit den kartesischen Koordinatenwerten, wenn wir den Kreisradius verdoppeln? Also nicht mehr fünf Längeneinheiten, sondern zehn Längeneinheiten? Bei genauer Zeichnung erkennt man, dass sich die Koordinatenwerte ebenso verdoppeln. Es zeigen sich die Eigenschaften einer zentrischen Streckung.
Der Einheitskreis
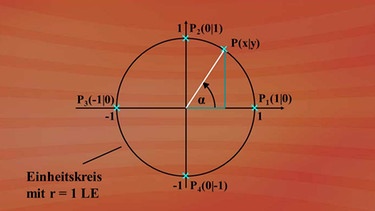
Ein Kreis mit dem Radius von einer Längeneinheit ist ein Einheitskreis. Was geschieht bei Abänderung von x-Koordinate und y-Koordinate eines Punktes P, der auf dem Einheitskreis wandert? Nebenstehend sehen Sie, wie das Bild dann aussieht - klicken Sie bitte auf die Lupe.
Der Punkt P, der in Abhängigkeit des Winkels α auf dem Kreis wandert, hat die kartesischen Koordinaten x und y. Für α = 0 Grad ergibt sich der Punkt P1 mit 1 und 0.
Für α = 90 Grad P2 mit 0 und 1.
Für α = 180 Grad P3 mit -1 und 0.
Und für α = 270 Grad der Punkt 0 und -1. Bei α = 360 Grad sind wir wieder bei P1.
Fazit:
x- und y-Koordinate des Punktes P ändern sich bei einem auf dem Kreisbogen wandernden P.