12. Sinus-, Kosinus- und Tangensfunktion 12.3. Sinus- und Kosinuskurve
Wir betrachten nur die Änderung der y-Koordinate des Punktes P.
Zugleich tragen wir die y-Werte in ein danebenliegendes Koordinatensystem ein - und zwar in Schritten von 30 Grad.
Die Sinuskurve
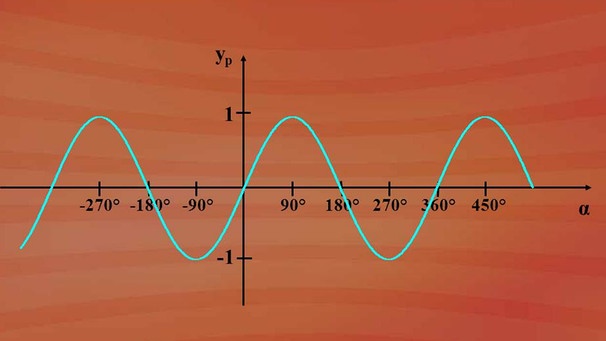
Die x-Achse trägt die α-Werte, die y-Achse die dazugehörigen y-Werte des Punktes P. Lässt man den Punkt P schrittweise wandern, und überträgt die y-Werte in dieses System, ergibt sich eine ganz besondere Kurve, die sogenannte Sinuskurve mit der Funktionsgleichung yp ist Sinus von α.
Durch die Sinusfunktion wird jedem Winkel eine Streckenlänge im Einheitskreis zugeordnet. Diese Zuordnung ergibt den gerade gesehenen Graph der Sinusfunktion. Warum die Bezeichnung Sinus gewählt wurde, ist nicht eindeutig nachvollziehbar. Der lateinische Begriff Sinus steht für Bogen, Krümmung oder Busen.
Sinusfunktion
Wir haben die Sinusfunktion für die Winkelmaße von 0 Grad bis 360 Grad erstellt. Man könnte dies aber auch über die 360 Grad hinaus weiterlaufen lassen. Für den Graphen bedeutet das eine periodische Fortsetzung. Man kann den Graphen aber auch für negative Winkelmaße fortsetzen. Es wird also immer nur ein Ausschnitt des vollständigen Graphen der Sinusfunktion gezeichnet.
Der Graph gleicht einer Wellenlinie, die für Winkelmaße von minus unendlich kommend bei plus unendlich periodisch verläuft.
Die Kosinuskurve
Als nächstes werden wir die Änderung der x-Koordinate des auf dem Einheitskreis wandernden Punktes P betrachten.
Die x-Achse trägt wiederum die α-Werte. Auf der Hochwertachse werden jetzt aber die x-Werte des Punktes P abgetragen. Bei α = 0 Grad hat die x-Koordinate des Punktes P den Wert 1. Danach wird der x-Wert kleiner, bis er bei 90 Grad den Wert 0 und bei 180 Grad den Wert -1 annimmt. Es entsteht die sogenannte Kosinuskurve. Sie ist der Graph für die Funktionsgleichung xp ist Kosinus von α.
Auch durch die Kosinusfunktion wird jedem Winkel α eine Streckenlänge zugeordnet. Und diese Zuordnung ergibt den Verlauf des gezeigten Graphen. Weshalb die Bezeichnung "Cosinus" gewählt wurde ist leichter nachzuvollziehen. Sie ergibt sich aus complementi sinus, was nichts anderes bedeutet als Sinus des Komplementärwinkels.
Zusammenfassung:
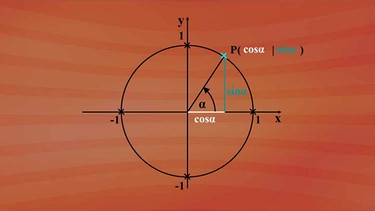
Kosinus von α und Sinus von α geben die kartesischen Koordinaten des Punktes P auf dem Einheitskreis an. Die x-Koordinate entspricht dem Wert von Kosinus α und die y-Koordinate dem Wert von Sinus α.
Natürlich muss man die Sinus- und Kosinuswerte nicht immer über eine Grafik ermitteln. Es gibt dazu Tabellenwerke, in denen diese Werte für bestimmte Winkel erfasst sind. Im Zeitalter des Taschenrechners sind diese Werte im Rechner gespeichert und können für jedes Winkelmaß abgerufen werden.
Tabellarische Darstellung
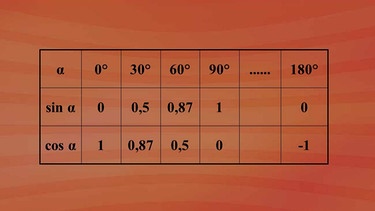
So sieht eine entsprechende Tabelle aus - klicken Sie bitte auf nebenstehende Grafik. In der ersten Zeile stehen die α-Werte. In der zweiten Zeile stehen die dazugehörigen Sinuswerte und in der dritten Zeile die dazugehörigen Kosinuswerte.
Man kann auch hier erkennen, dass Sinus und Kosinus nur Werte zwischen -1 und +1 annehmen.
Punkte außerhalb des Einheitskreises
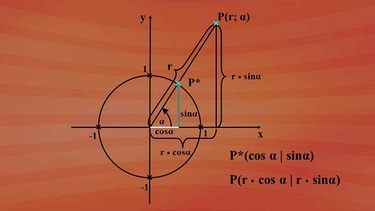
Wie bekommt man aus Polarkoordinaten von Punkten, die nicht auf dem Einheitskreis liegen, die kartesischen Koordinaten? Zum Beispiel ein Punkt P mit den Polarkoordinaten r und α: Wäre der Punkt auf dem Einheitskreis -nennen wir den angenommenen Punkt P Stern - hätte er die Koordinaten Kosinus α für x und Sinus α für y.
Über die zentrische Streckung vom Ursprung 0 aus hat dann der Punkt P die Koordinaten r ·Kosinus α und r · Sinus α.
Somit können alle Punkte, die im Polarkoordinatensystem mit Abstand vom Ursprung und Winkelangabe α dargestellt sind, in kartesische Koordinatenwerte umgerechnet werden. Auch die zwölf Sterne auf der Europaflagge.