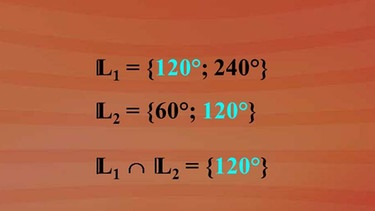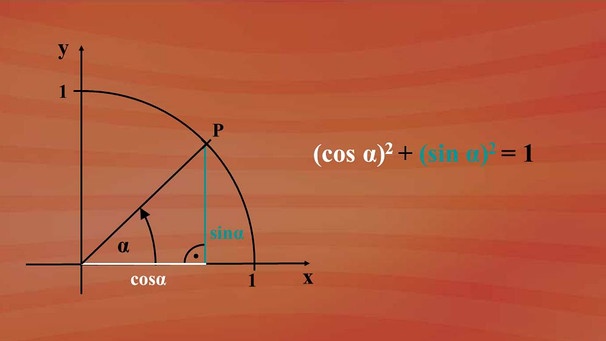
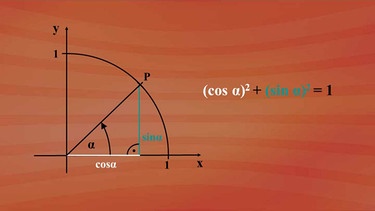
Die Strecken für Kosinus alpha und Sinus alpha bilden mit dem Einheitskreisradius eins ein rechtwinkliges Dreieck.

Sinus alpha und Kosinus alpha als Katheten im Lehrsatz von Pythagoras

Sinus alpha und Kosinus alpha sind dabei Katheten und der Radius die Hypotenuse. Somit gilt nach dem Lehrsatz von Pythagoras: Kathete eins, also Kosinus alpha, zum Quadrat, plus Kathete zwei mit Sinus alpha zum Quadrat ist gleich Hypotenuse, hier Radius eins, zum Quadrat. Und eins zum Quadrat bleibt eins.

Beispiel zum Einheitskreis

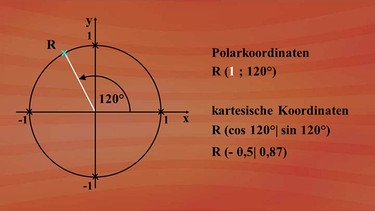
Ein Punkt R hat die Polarkoordinaten eins und 120°. Das heißt, er liegt am Einheitskreis. Es ist ein Leichtes, die kartesischen Koordinaten zu bestimmten: Kosinus 120° für die x-Koordinate und Sinus 120° für die y-Koordinate. Mit dem Taschenrechner ausgerechnet: minus 0,5 und 0,87.

Bestimmung der Polarkoordinaten

Wäre es auch möglich, aus den kartesischen Koordinaten eines Punktes am Einheitskreis die Polarkoordinaten zu bestimmen?

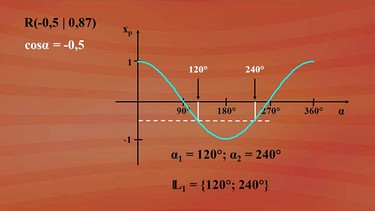
Die erste Polarkoordinate ist einfach: Einheitskreis bedeutet r gleich eins. Aber wie kommt man auf das Winkelmaß alpha? Bleiben wir bei unserem Punkt R mit -0,5 und 0,87. Die x-Koordinate ist nichts anderes als der Kosinuswert des Winkels.

Also Kosinus alpha ist minus 0,5. Es ergibt sich der Wert 120 Grad, was richtig ist. Aber auch 240 Grad wären als Lösung korrekt. Und auch noch weitere Winkelmaße auf Grund der Periodizität kämen in Frage.

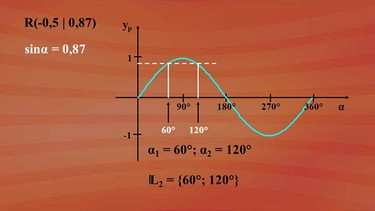
Es gibt noch ein zweites Bestimmungsstück für den Punkt R. Er hat die y-Koordinate 0,87. Die y-Koordinate ist der Sinuswert des Winkels alpha - er wird an der entsprechenden Kurve, hier der Sinuskurve, abgelesen. Der Sinuswert 0,87 liefert im Winkelfeld von 0 Grad bis 360 Grad die Winkelmaße 60 Grad und 120 Grad.

Der wahre Wert für das Winkelmaß

Was ist jetzt der wahre Wert für das Winkelmaß?

Es ist die Schnittmenge aus den beiden Lösungsmengen L1 und L2. Das Element 120 Grad ist in beiden Lösungsmengen enthalten und bildet somit das Lösungselement.

Das Bogenmaß

Wir haben unsere Winkelgrößen bisher in Grad angegeben, wie zum Beispiel unser Lösungselement mit 120 Grad. In vielen Teilbereichen der Mathematik und besonders in technischen Aufgabenbereichen verwendet man für die Angabe von Winkelmaßen das Bogenmaß.

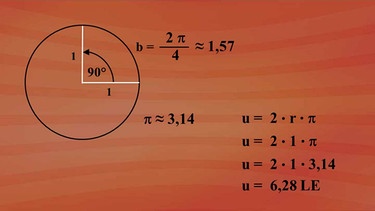
Beim Bogenmaß gibt die Maßzahl der zu einem Winkel gehörenden Bogenlänge auf dem Einheitskreis die Größe des Winkels an. Der gesamte Kreisumfang beträgt nach der Formel u gleich zwei mal Radius mal Kreiszahl Pi für den Einheitskreis u gleich zwei mal eins mal Pi gleich 6,28 Längeneinheiten.

Bei 90 Grad beträgt die Bogenlänge ein Viertel des Gesamtbogens und somit geteilt durch vier gleich ungefähr 1,57 Längeneinheiten.