Multiplikation von Summen, Binome Multiplikation einer algebraischen Summe
Nun können wir eine Gesetzmäßigkeit formulieren, wie algebraische Summen allgemein mit einem Faktor multipliziert werden. Sie lautet:
Formel:
Eine algebraische Summe wird mit einem Faktor multipliziert, indem man jedes Glied der Summe mit dem Faktor multipliziert.
Da die Subtraktion die Addition eines negativen Wertes ist, gilt die Gesetzmäßigkeit auch für Differenzen. Dazu benötigen wir wieder unsere Vorzeichenregeln, die für die Multiplikation Gültigkeit haben:
| 1. Faktor | 2. Faktor | Produktwert |
|---|---|---|
| + | + | + |
| - | - | + |
| + | - | - |
| - | + | - |
Beispiel
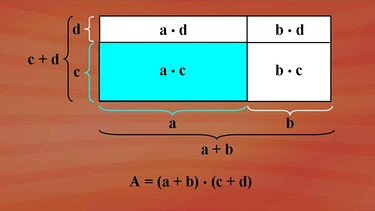
Wir wählen eine Rechtecksfläche mit den Seitenlängen a und c. Wir gehen davon aus, dass es sich bei allen Variablen um Größen der gleichen Einheit handelt. Die Seite a verlängern wir um b und die Seite c um d. Die neue Rechtecksfläche besitzt die Fläche a plus b in Klammern mal c plus d in Klammern. Und schon haben wir die Multiplikation von zwei algebraischen Summen.
In dem Zahlenbeispiel wurde jedes Glied der ersten Klammer mit jedem Glied der zweiten Klammer unter Berücksichtigung der Vorzeichenregeln multipliziert. Hier haben wir nur gleiche Vorzeichen, also haben die Teilergebnisterme alle positives Vorzeichen.Groß A ist a mal c plus a mal d plus b mal c plus b mal d. Als Gesetzmäßigkeit ergibt das:
Gesetzmäßigkeit:
Zwei algebraische Summen werden miteinander multipliziert, indem man jedes Glied der ersten Summe mit jedem Glied der zweiten Summe unter Berücksichtigung der Vorzeichenregel multipliziert und die Ergebnisse addiert.