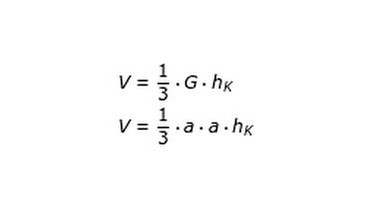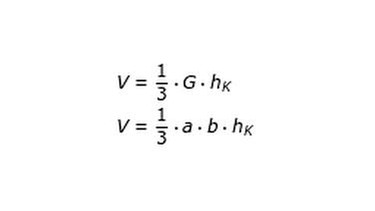GRIPS Mathe 24 Wie berechnest du das Volumen von geraden Pyramiden?
Eine Pyramide und ein Quader haben die gleiche Grundfläche und die gleiche Höhe. Wie oft passt das Volumen der Pyramide in das Volumen des Quaders?
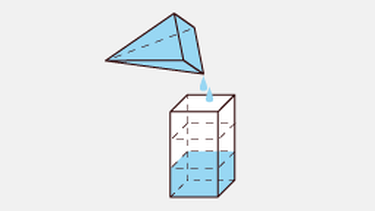
Der "Umschüttversuch"
Dazu machen wir einen Versuch. Wir füllen die Pyramide mit einer farbigen Flüssigkeit und probieren aus, wie oft die Flüssigkeit der Pyramide in den Quader passt.
Was denkst du?
Wie oft passt die Flüssigkeit des Quaders (rechts) in die Pyramide (links)?
Lösung: Der Inhalt der Pyramide passt 3-mal in den Quader.
Klicke auf die Lupe, um den den kompletten "Umschüttversuch" zu sehen.
Man kann auch sagen: Das Volumen der Pyramide ist ein Drittel so groß wie das Volumen des Quaders.
Aus diesem Umschüttversuch kannst du die allgemeine Formel für die Volumenberechnung einer Pyramide ableiten:
Volumen Pyramide
Diese allgemeine Formel solltest du dir merken:
Volumen der Pyramide = 1/3 · Grundfläche · Höhe des Körpers
VPyramide = 1/3 · G · hK
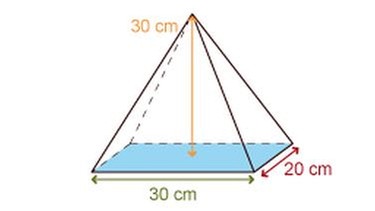
Für die unterschiedlichen Pyramiden brauchst du nur die allgemeine Formel an die Grundfläche der Pyramide anzupassen. Beachte dabei immer diese drei Schritte:
1. Schritt: Beachte immer zuerst die allgemeine Grundformel: V = 1/3 · G · hK
2. Schritt: Setze dann in die allgemeine Formel die passende Formel für die Grundfläche G der Pyramide ein.
3. Schritt: Multipliziere das Ergebnis mit der Höhe der Pyramide.
Beispiele:
Volumen: Quadratische Pyramide
Pyramide
Hier siehst du eine quadratische Pyramide.
Sie heißt quadratische Pyramide, da ihre Grundfläche ein Quadrat ist.
Seitenlänge a = 20 cm
Höhe h = 30 cm
Volumen: Rechteckspyramide
Pyramide
Hier siehst du eine Rechteckspyramide.
Sie heißt Rechteckspyramide, da ihre Grundfläche ein Reckteck ist.
Seitenlänge a = 30 cm
Seitenlänge b = 20 cm
Höhe h = 30 cm
Volumen: Dreieckspyramide
Pyramide
Hier siehst du eine Dreieckspyramide.
Sie heißt Dreieckspyramide, da ihre Grundfläche ein Dreieck ist.
Grundseite des Dreiecks = 20 cm
Höhe des Dreiecks = 15 cm
Höhe der Pyramide = 30 cm
