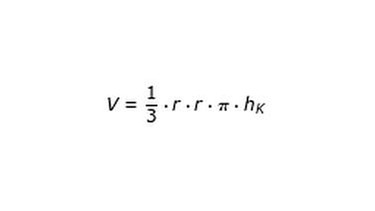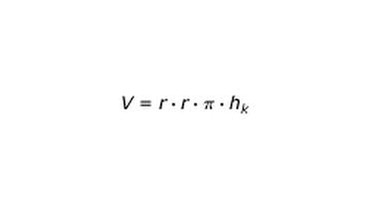GRIPS Mathe 24 Wie gehst du bei zusammengesetzten Körpern vor?
Für eine Bar werden Eckpfosten in einer bestimmten Form benötigt. Diese werden an einer Drehbank in einer Werkstatt angefertigt.
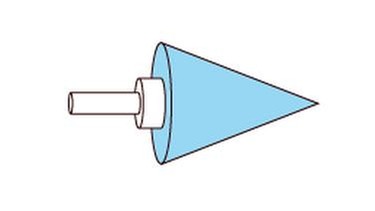
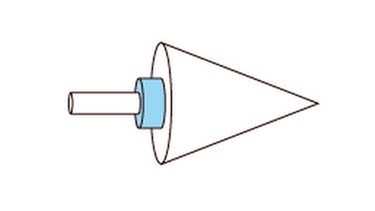
Auf dem Bild siehst du, wie die Eckpfosten aussehen. Sie bestehen aus zwei Körpern.
Vorne kannst du einen Kegel erkennen (die Spitze). Hinten angesetzt ist ein Zylinder.
Wie berechnest du das Volumen dieses Körpers?
Bei Abschlussprüfungen kommt es oft vor, dass du mit solchen zusammengesetzten Körpern rechnen musst. Dann musst du dir ein passendes Lösungsschema ausdenken.
Lösungsschema für zusammengesetzte Körper
Klicke auf die Lupe, um den zusammengesetzen Körper und seine Maße zu sehen!
In dieser Abbildung siehst du einen Zylinder und einen Kegel. Diese beiden Körper werden zu einem Körper zusammengesetzt.
Wie groß ist das Volumen des zusammengesetzten Körpers?
Um das Volumen des gesamten Körpers zu ermitteln, berechnest du zunächst das Volumen des Zylinders (Körper 1) und des Kegels (Körper 2). Anschließend addierst du die beiden Ergebnisse:
| Volumen Zylinder | Volumen Kegel | Volumen Gesamtkörper |
|---|---|---|
| = r · r · Pi · hK | = 1/3 · r · r · Pi · hK | |
| = 2 · 2 · 3,14 · 3,5 | = 1/3 · 2 · 2 · 3,14 · 8 | |
| = 43,96 cm³ | = 33,52 cm³ | |
| = 77,48 cm³ |
Beispiele aus den Abschlussprüfungen
Wir zeigen dir nun anhand von zwei Beispielen aus den Abschlussprüfungen, wie du das Volumen eines zusammengesetzten Körpers berechnen kannst.
Zuerst überlegst du dir ein Lösungsschema. Das bedeutet, du überlegst dir aus welchen Teilkörpern der Gesamtkörper besteht. Dann berechnest du das Volumen jedes Teilkörpers und am Schluss addierst du das Volumen der einzelnen Körper.
Beispiel 1:
Flaschenverschluss
Ein moderner Flaschenverschluss aus Edelstahl (Dichte: 8,5 g/cm³) verschließt die Flasche durch sein Eigengewicht.
Wie schwer ist er?
Berechne zunächst das Volumen des Flaschenverschlusses und dann die Masse.
Hinweis: Rechne mit Pi = 3,14! Runde Teilergebnisse auf zwei Dezimalstellen.
Masse und Volumen berechnen
Lösungsschema: Zusammenzählen der Teilkörper Kegel, Zylinder und Quader
Rechenweg
Kegel
Volumen Kegel
Werte aus der Abbildung in die Formel einsetzen:
V= 1/3 · 1,5 · 1,5 · 3,14 · 4
V= 9,42 cm³
Beispiel 2:
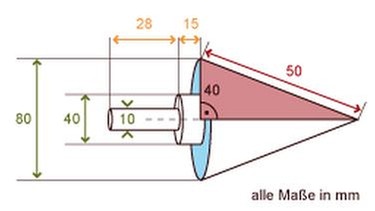
Kreisel
Bei einem Spielwarenhersteller werden Kreisel aus Edelstahl hergestellt.
a. Berechne die Gesamthöhe des Kreisels.
b. Wie schwer ist der Kreisel? (Dichte Edelstahl: 8,5 g/cm³)
2a. Gesamthöhe des Kreisels
Lösungsschema: Addition aller Höhenangaben
a. Gesamthöhe des Kreisels
Höhe des Kegels
Höhe des Kegels mit dem Satz des Pythagoras:
a² + b² = c²
a² + 40² = 50² / - 40²
a² = (50 · 50) - (40 · 40)
(Achtung, nicht: 50² - 40² = 10²)
a² = 900 / Wurzel ziehen
a = 30 mm
2b. Masse des Kreisels
Lösungsschema: Zusammensetzen der einzelnen Teilkörper
b. Masse des Kreisels
Kegel
Volumen Kegel
Werte aus der Abbildung in die Formel einsetzen:
V= 1/3 · 40² · 3,14 · 30
V= 50240 mm³
