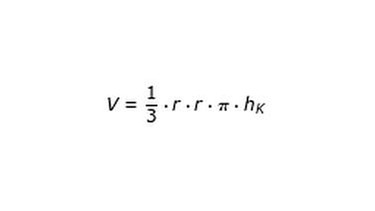GRIPS Mathe 24 Wie berechnest du das Volumen von Kegeln?
Ein Kegel und ein Zylinder haben die gleiche Grundfläche und die gleiche Höhe. Wie oft passt das Volumen des Kegels in das Volumen des Zylinders?
Der "Umschüttversuch"
Genau wie bei den Pyramiden machen wir auch hier den "Umschüttversuch". Wir füllen den Kegel mit einer farbigen Flüssigkeit und probieren aus, wie oft die Flüssigkeit des Kegels in den Zylinder passt. Was denkst du?
Lösung: Der Inhalt des Kegels passt 3-mal in den Zylinder.
Wieder kannst du aus dem Umschüttversuch die allgemeine Formel ableiten:
Volumen Kegel
Diese allgemeine Formel solltest du dir merken:
Volumen des Kegels = 1/3 · Grundfläche · Höhe des Körpers
Die Grundfläche des Kegels ist ein Kreis. Das Volumen eines Kegels berechnest du daher mit dieser Formel:
VKegel = 1/3 · r · r · Pi · hK
Die nächsten beiden Beispiele zeigen dir, wie du mit unterschiedlichen gegebenen Werten das Volumen eines Kegels berechnest:
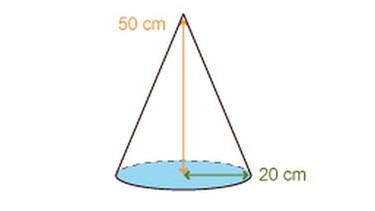
Beispiel 1:
Volumen Kegel
Kegel
Ein Kegel ist ein Spitzkörper mit einem Kreis als Grundfläche.
Höhe h des Kegels = 50 cm
Radius r des Kreises = 20 cm
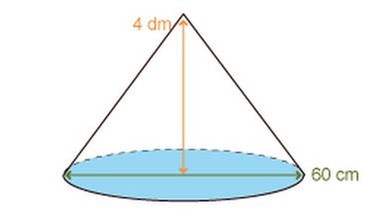
Beispiel 2:
Wenn du das Volumen des nächsten Kegels berechnest, musst du zwei Punkte beachten:
1. Die Einheiten müssen gleich sein. Wandle zum Beispiel die Dezimeter in Zentimeter um!
2. Wenn der Durchmesser gegeben ist, rechne auf den Radius zurück:
Durchmesser = 2 · Radius bzw. Radius = Durchmesser : 2
Volumen Kegel
Kegel
Ein Kegel ist ein Spitzkörper mit einem Kreis als Grundfläche.
Höhe h des Kegels = 4 dm
Durchmesser d des Kreises = 60 cm