GRIPS Mathe 30 Dreiecke
Dreiecksformen
Dreieck ist nicht gleich Dreieck. Du kannst Dreiecke je nach Seitenlänge und Winkel unterscheiden:
Dreiecke und ihre Eigenschaften
stumpfwinklig
Stumpfwinklige Dreiecke
Ein Winkel ist größer als 90°.
Dreiecke zeichnen und konstruieren
Wenn du ein Dreieck konstruieren sollst, können die Angaben in der Aufgabenstellung ganz unterschiedlich sein. Entweder es sind nur die Seitenlängen gegeben oder Winkel und Seitenlänge. Wir schauen uns drei Möglichkeiten an:
Konstruktion eines Dreiecks bei...
- drei gegebenen Seitenlängen (SSS)
- zwei gegebenen Seitenlängen und ihrem Winkel (SWS)
- zwei gegebenen Winkeln und einer Seitenlänge (WSW)
Zur Konstruktion der Dreiecke benötigst du ein Geodreieck, einen Zirkel, Papier und einen Bleistift.
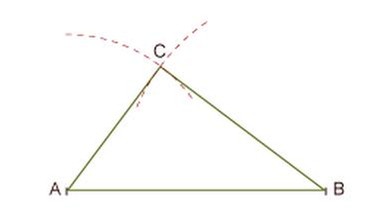
a. Dreieck aus drei Seiten (SSS)
Zeichne ein Dreieck mit den Seiten a = 4 cm, b = 3 cm und c = 5 cm.
Lösung
Schritt 1
Zeichne die Strecke [AB].
Die Strecke [AB] entspricht der Seite
c = 5 cm.
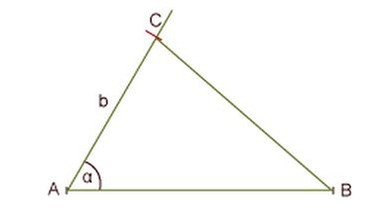
b. Dreieck aus zwei Seiten und einem Winkel (SWS)
Gegeben ist ein Dreieck mit c = 6 cm, α = 60°, b = 4 cm.
Lösung
Schritt 1
Zeichne die Strecke [AB].
Die Strecke [AB] entspricht der Seite
c = 6 cm.
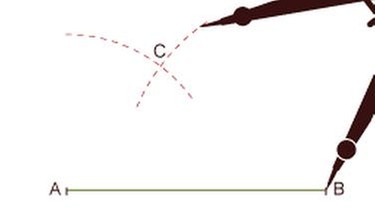
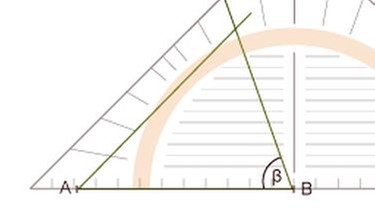
c. Dreieck aus zwei Winkeln und einer Seite (WSW)
Gegeben ist ein Dreieck mit c = 5,5 cm, α = 45°, β = 70°.
Lösung
Schritt 1
Zeichne die Seite c = 5,5 cm mit den Endpunkten A und B.
