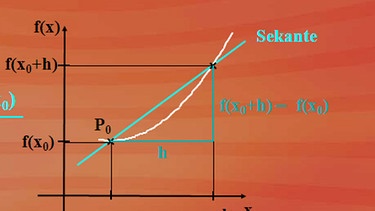
Die Grundableitungsregel ist ein wichtiger, vielleicht sogar der wichtigste Teil der Differentialrechnung. Wir tasten uns mit einfachen Beispielen an sie heran. Am Ende der Lektion sind Ableitungen kein Problem mehr für Sie.

Oben können Sie das Video der komplettten Sendung noch einmal ansehen - klicken Sie auf den Pfeil.