Differentialrechnung Prüfung mittels Steigungsfunktion
Wir betrachten noch einmal lineare und konstante Funktionen näher und testen, ob unsere bisherigen Erkenntnisse einer Prüfung mittels Steigungsfunktion standhalten.
Ist die Ableitungsfunktion jeder linearen Funktion wirklich die konstante Funktion f'(x) = m? Das prüfen wir nochmals an einem beliebig gewählten Beispiel.
Beispiel
Wir nehmen die lineare Funktion f(x) = 1/2 x + 2. Grafisch dargestellt lässt sich die Steigung ein halb schön ablesen. Die Ableitungsfunktion ist dann f'(x) = 1/2. Ob diese Ableitungsfunktion richtig ist, werden wir mittels Sekantensteigung und Tangentensteigungsfunktion nochmals überprüfen.
Überprüfung
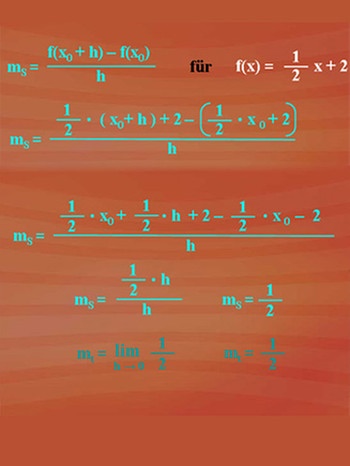
Die Formel für die Sekantensteigung ist Ihnen mittlerweile vertraut. Angewandt für die Funktion f(x) = 1/2 x + 2 ergibt sich nebenstehender Ausdruck für ms. Den weiteren Rechenweg mit Ausmultiplizieren, Zusammenfassen und Kürzen sehen Sie bei Klick auf die Abbildung. Wir erhalten die Sekantensteigung mit ein halb, und somit auch die Tangentensteigung mit ein halb. Unsere Überprüfung hat die angenommene Vermutung bestätigt.
Konstante Funktionen
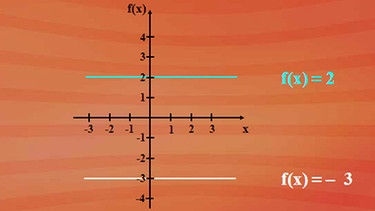
Obenstehende Aussage ist logisch zu erklären - betrachten Sie nur die Steigung von konstanten Funktionen: zum Beispiel die konstante Funktion f(x) = 2, oder f(x) = - 3. Ihre Graphen sind Parallelen zur x-Achse und haben somit die Steigung null. Steigung null bedeutet, dass die Ableitung jeder konstanten Funktion die Nullfunktion ist. Es hat also die Funktion f(x) = 263,48 die Ableitung f'(x) = 0.
Zusammenfassung
Die lineare Funktion f(x) gleich m mal x plus t hat die Ableitungsfunktion f'(x) gleich m. Das heißt, der konstante Summand - bei uns mit dem Platzhalter t symbolisch dargestellt - wird bei der Ableitung null.