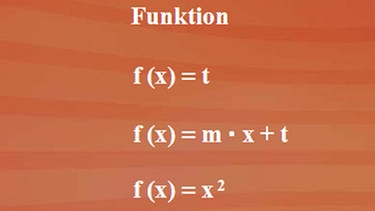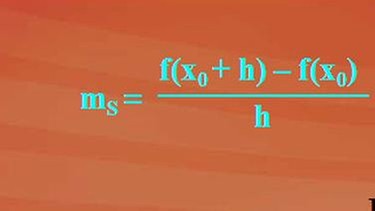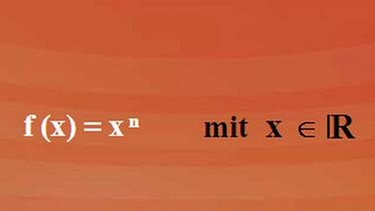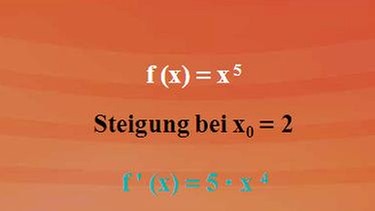Denken Sie daran: Das Wichtigste ist immer in der Formelsammlung zu finden - auch das, worum es jetzt in einer ersten kleinen Zusammenfassung von Ableitungen einiger Potenzfunktionen geht. Zuvor aber noch eine Frage: Wissen Sie, was eine Potenzfunktion ist?

Ableitungen verschiedener Funktionen

Funktion und Ableitung - klicken Sie bitte auf die Lupe

Nach dieser Definition ist die konstante Funktion keine Potenzfunktion. Wir wollen aber trotzdem die Ableitung in die angekündigte Zusammenstellung mit aufnehmen. So hat die konstante Funktion f(x) = t die Ableitungsfunktion f'(x) = 0. Bei Klick auf nebenstehendes Bild sehen Sie die Ableitungen für weitere Funktionen.

Es wäre natürlich schön, wenn irgendeine Gesetzmäßigkeit dahinterstecken würde. Dann könnte man sich den umständlichen Weg über die Sekanten- und Tangentensteigung sparen. Lassen Sie uns deshalb den Funktionsterm mit seinem dazugehörigen Ableitungsterm noch einmal genauer betrachten.

Funktionsterm und Ableitungsterm

Funktionsterm und Ableitungsterm - klicken Sie bitte auf die Lupe

Für den Funktionsterm t der konstanten Funktion denken wir uns den Faktor hoch null dazu, denn dieser Faktor x hoch null verändert am Termwert nichts, da irgendetwas hoch null gleich 1 ist. Der Ableitungsterm ist null. Weiter gibt jeder Funktionsterm m mal x den Ableitungsterm m. Der Faktor x könnte auch als x¹ angeschrieben werden. Die Hochzahl 1 schreiben wir nur üblicherweise aus Bequemlichkeitsgründen nicht dazu. Der quadratische Term x² geht in den Ableitungsterm 2 mal x über und der kubische Term x³ in den Ableitungsterm 3 mal x². Damit Sie sich beim Finden einer Gesetzmäßigkeit leichter tun, ergänzen wir noch den Faktor 1 vor m, da 1 mal m äquivalent zu m ist. Und beim Faktor x im Produkt 2 mal x ergänzen wir die Hochzahl 1. Welchen Ableitungsterm könnte nun der Funktionsterm x⁴ haben? Die Vermutung ist: 4 mal x³.

Weitere Überlegungen

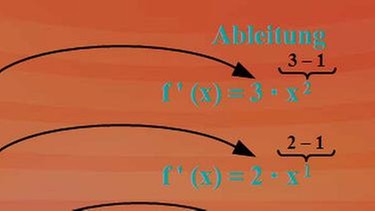
Für die weiteren Überlegungen klicken Sie bitte auf nebenstehendes Bild. Bei f(x) = x³ wurde für die Ableitung die Zahl 3 im Exponenten als Faktor nach vorne gezogen, und zugleich die Hochzahl um 1 vermindert. Die Ableitung lautet somit 3 mal x².
Gleiches geschah bei f(x) = x². Die Hochzahl 2 kam als Faktor nach vorne und wurde zugleich um 1 vermindert.
Auch bei f(x) = m mal x¹ klappt es. Die Hochzahl 1 kommt nach vorne und gibt um 1 vermindert null. Und wie Sie wissen, ist irgendetwas hoch null gleich eins. Dann bleibt 1 mal m mal 1 als m stehen.
Bei der konstanten Funktion f(x) = t klappt dieses Spielchen, wenn man sich bei dem Platzhalter t als Faktor x₀ dazu denkt. Die Hochzahl null kommt nach vorne und wird um 1 vermindert. Und null mal irgendwas ist null.

Weitere Überlegungen zu Funktion und Ableitung - klicken Sie bitte auf die Lupe

Jetzt müssten Sie eigentlich die Ableitung der Funktion f(x) = x⁴ selbst bestimmen können - nur mit dem Wissen, Hochzahl kommt nach vorne und wird um 1 vermindert. Dann ist die Ableitung der Funktion f(x) = x⁴: f'(x) = 4 mal x³. Ob das richtig ist, überprüfen wir jetzt noch mittels der Sekantensteigung.

Prüfung mittels Sekantensteigung

Steigung der Sekante - klicken Sie bitte auf die Lupe

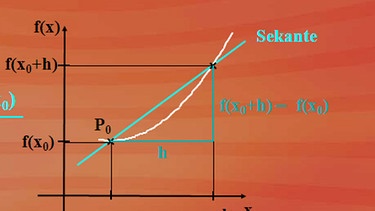
Die Formel für die Steigung der Sekante durch die Punkte x₀ und x₀ plus h des Graphen einer Funktion sehen Sie bei Klick auf nebenstehende Abbildung. Grafisch dargestellt, ist das im Grunde nichts anderes als die Steigungsbestimmung über das Steigungsdreieck.

Berechnung der Sekantensteigung - klicken Sie bitte auf die Lupe

Jeder Punkt des Graphen hat die Koordinaten x und f(x) - ein beliebig ausgewählter Punkt P₀ eben x₀ und f(x₀). Bei der Funktion f(x) = x⁴ hat ein ausgewählter Punkt dann die Koordinaten x₀ und x₀⁴. Ab jetzt bedarf es besonderer mathematischer Umformungen. Sie führen nur dann zum erhofften Erfolg, wenn man das Ziel, hier die Bestimmung der Tangentensteigung, stets im Auge hat. Den weiteren Rechenweg sehen Sie hier:

Soweit die Berechnung - da unser Ergebnis für jede Stelle x null Element aus dem reellen Zahlenbereich Gültigkeit hat, ist unsere Behauptung, dass die Funktion f(x) = x⁴ die Ableitung 4 mal x³ besitzt, somit bewiesen. Auch unsere gefundene Ableitungsregel, dass die Hochzahl nach vorne genommen und um eins vermindert wird, hat sich bewahrheitet. Allgemein können wir folgern:

Wie lautet die Ableitung nebenstehender Funktion? Klicken Sie bitte auf die Lupe.

Eine Funktion f(x) = xⁿ hat für alle x Element aus R die Ableitung f'(x) = n mal xⁿ minus 1. Und weiter wissen wir noch, dass diese Ableitung die Steigung eines jeden Punktes x₀ der Funktion angibt.

Übungsaufgabe

Wie ist die Aufgabe aus dem Video zu lösen? Wir wissen bereits, wie das ohne Zeichnung auf Millimeterpapier möglich ist. Denn wir haben gelernt, dass die Ableitung der Funktion die Steigung in jedem beliebigen Punkt des Graphen der Funktion angibt.
Die Funktion lautet f(x) = x⁵. Gefragt ist die Steigung an der Stelle x₀ = 2.

Ableitung der Funktion - bitte klicken Sie auf die Lupe

Wir müssen also zuerst die Ableitung bilden - siehe nebenstehende Abbildung. Die Hochzahl, also die 5, kommt nach vorne, und zugleich wird die Hochzahl um 1 vermindert.
Da die erste Ableitung die Steigung in jedem Punkt der Ausgangsfunktion angibt, haben wir f' an der Stelle x₀ = 2 zu berechnen. Wie das geht, sehen Sie bei Klick auf die Abbildung. Wir müssen also keine Tangente mit der Steigung 80 Eintel - also eine Einheit nach rechts und 80 Einheiten nach oben - einzeichnen.

Sie sehen, welche Erleichterung sich durch die Grundableitungsregel bei der Bestimmung von - vorerst - Steigungen ergibt!