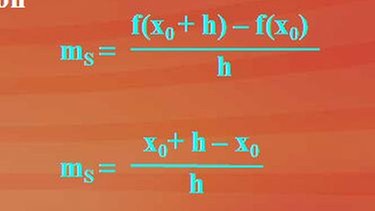Differentialrechnung Steigung linearer Funktionen
Jetzt befassen wir uns mit linearen Funktionen und dem "Sekantenproblem": Wir wollen über die Sekantensteigungsfunktion theoretisch nachweisen, dass eine lineare Funktion für alle Punkte nur eine gleichbleibende Steigung hat.
Lineare Funktionen haben die Funktionsgleichung f(x) gleich m mal x plus t mit konstanten Werten für m und t. Der Faktor m gibt bekanntlich die Steigung der Geraden an. Und hier haben wir schon das Besondere. Die lineare Funktion hat für alle Punkte nur eine gleichbleibende Steigung. Das wollen wir über die Sekantensteigungsfunktion theoretisch nachweisen. Wir haben jetzt kein Tangentenproblem, sondern ein Sekantenproblem.
Sekante
Unter einer Sekante versteht man eine Gerade, die durch mindestens zwei verschiedene Punkte einer Kurve oder eines Funktionsgraphen geht.
Die Tangente an die Gerade g muss also die Gerade sein, welche unendlich viele gemeinsame Punkte mit g hat. Somit muss es auch möglich sein, die Steigung der Geraden über die Tangentensteigungsfunktion zu bestimmen. Beginnen wir mit der Sekantensteigung.
Die Sekantensteigung
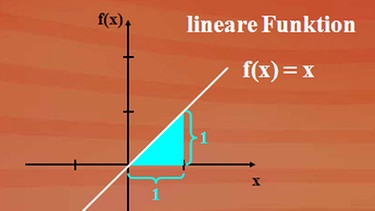
Wir wählen die einfachste lineare Funktion f(x) = x. Die Sekantensteigung ms berechnen wir nach nebenstehender Formel. Nach Umformen und Kürzen ergibt sich ms = 1.
Die Tangentensteigung
Wir wissen auch noch, dass die Tangentensteigung der Grenzwert der Sekantensteigungsfunktion ist. Die Tangentensteigung mt ist Limes h gegen null von ms. (Klicken Sie bitte auf nebenstehende Abbildung.) Unser ermitteltes ms eingesetzt, erhalten wir mt gleich Limes h gegen null von 1. Da der Term 1 von h unabhängig ist, ist auch der Limes dieser konstanten Zahl gleich 1. Die Steigung der Tangente ist gleich 1.
Dieses Ergebnis ist für uns nicht verwunderlich, da die Tangente einer linearen Funktion der linearen Funktion selbst entspricht. Das bedeutet dann, dass die Ableitungsfunktion jeder linearen Funktion die konstante Funktion f'(x) = m ist.