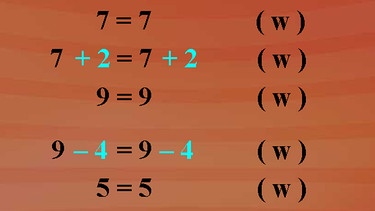Grundkurs Mathematik (4) 4.2. Äquivalenz von Gleichungen
Wie kann man allgemein die Variable mathematischer Gleichungen so bestimmen, dass eine wahre Aussage entsteht?
Dazu wollen wir uns die mathematische Gleichung als Waage vorstellen, bei der die linke Waagschale den Linksterm und die rechte Waagschale den Rechtsterm der Gleichung trägt.
Voraussetzung für Äquivalenz
Fazit: Die Waage bleibt im Gleichgewicht, wenn auf der linken und der rechten Waagschale gleiche Operationen durchgeführt werden. Ändert man auf den Waagschalen die Wertigkeiten so, dass die Waage im Gleichgewicht bleibt, so spricht man von "Äquivalenz". Voraussetzung dafür ist, dass bei der Änderung der Wertigkeiten die vorhandene Definitionsmenge nicht verändert wird.
Merksatz: Äquivalent – nicht äquivalent
Zwei Gleichungen mit Variablen heißen zueinander äquivalent, wenn sie gleiche Definitionsbereiche und gleiche Lösungsmengen haben. Andernfalls sind die Gleichungen nicht äquivalent.
Wann bleiben Aussagen wahr?
Eine wahre Aussage ist zum Beispiel: 7 ist 7. Das ist sicher mathematisch eine wahre Aussage. Eine neue wahre Aussage entsteht, wenn auf beiden Seiten die Zahl 2 addiert wird. Nämlich 9 ist 9. Subtrahieren wir auf beiden Seiten die Zahl 4, so erhalten wir wieder eine wahre Aussage: 5 ist 5. Multiplizieren wir beide Seiten mit 6, bleibt die Aussage auch wahr: 30 ist 30. Und das versuchen wir auch noch für die Division, also geteilt durch 10, so liefert uns dies die wahre Aussage 3 ist 3. Auch potenzieren können wir noch beide Seiten, zum Beispiel hoch 2 und erhalten wiederum eine wahre Aussage: 9 ist 9.
Wann bleiben Aussageformen äquivalent?:
Aussageformen bleiben dann äquivalent, wenn auf beiden Seiten mit derselben Zahl addiert oder subtrahiert wird. Sie bleiben auch äquivalent, wenn beide Seiten mit derselben Zahl multipliziert oder dividiert werden, wobei hier die Zahl 0 ausgeschlossen bleiben muss.