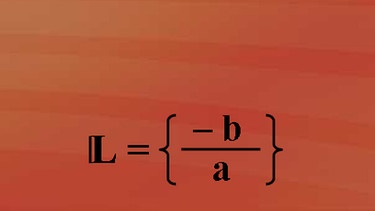Gleichung mit einer Variablen - klicken Sie bitte auf die Lupe

Wir wollen jetzt eine allgemeine lineare Gleichung mit einer Variablen lösen, zum Beispiel: a mal x plus b ist Null. Wobei a und b Platzhalter für beliebige rationale Zahlen sind, also für 3 oder -5 oder 283,4 und so weiter. Wir schreiben dafür a, b sind Elemente von Q, dem Symbol für die Menge der rationalen Zahlen. Für a müssen wir noch fordern, dass es ungleich Null ist, da bei a gleich Null automatisch die Aussageform in eine Aussage verwandelt würde. Denn x ist unsere Gleichungsvariable. Ihre Definitionsmenge ist in der Grundmenge zu suchen, in unserem Falle jetzt G für Grundmenge gleich Q. Es bedeutet, dass als Lösung für die Gleichungsvariable x nur rationale Zahlen in Frage kommen.

Lösung der linearen Gleichung

Wir wollen nun die allgemeine Lösung der linearen Gleichung ermitteln. Dies geschieht dadurch, dass wir solange äquivalent umformen, bis die Gleichungsvariable x allein auf einer Seite der Gleichung steht.

Gleichungsvariable - klicken Sie bitte auf die Lupe

Alles, was um die Gleichungsvariable herumsteht, müssen wir beseitigen. Das geschieht zuerst einmal, indem wir auf beiden Seiten b subtrahieren. Es bleibt a mal x ist minus b. Jetzt steht vor dem x noch ein a. Teilen wir aber auf beiden Seiten der Gleichung durch a, so erkennen wir, dass sich die Variable a auf der linken Seite der Gleichung wegkürzt und nur noch die Gleichungsvariable x als 1 mal x stehen bleibt. Auf der rechten Seite der Gleichung ergibt sich der Quotient minus b durch a. Und dieser Quotient bildet das Lösungselement der Gleichung, welches in die Lösungsmenge aufgenommen wird.

Die Lösungsmenge zeigt uns, dass die behandelte lineare Gleichung für alle a und b Element von Q und a ungleich Null eine eindeutige Lösung besitzt. Ändert man die Grundmenge für die Variablen, so kann es durchaus möglich sein, dass x minus b durch a auch mal keine Lösung hat oder eine allgemeine gültige Aussage darstellt.

Lösen einer Gleichung mit einer Variablen

Ein Beispiel: 4 x plus 3 mal x plus 1 in Klammern plus 2 ist gleich 2 mal x minus 2 in Klammern plus 3x plus 3. Als Grundmenge für die Gleichungsvariable x wählen wir die Menge der ganzen Zahlen Z. Zuerst werden jetzt beide Seiten möglichst weit vereinfacht.

Anwendung: Vereinfachung von Termen

Jetzt können wir anwenden, was wir über die Vereinfachung von Termen bereits gelernt haben. Die linke Seite der Gleichung können wir als Linksterm und die rechte Seite der Gleichung als Rechtsterm betrachten. Das Schlagwort war damals Klapps. Klammerrechnung vor Punkt- und Potenzrechnung und das wieder vor der Strichrechnung. Also zuerst das Ausmultiplizieren der Klammern.

Erster Rechenschritt

1. Beide Seiten möglichst weit vereinfachen

Der Faktor vor der Klammer wird mit den Gliedern in der Klammer unter Berücksichtigung der Vorzeichenregeln multipliziert. Den ausführlichen ersten Rechenschritt sehen Sie, wenn Sie auf nebenstehende Grafik klicken. Nun müssen wir so lange umformen, bis die Variable x alleine auf einer Seite der Gleichung steht.

Zweiter Rechenschritt

2. Variable auf eine Seite bringen

Wir subtrahieren nun im zweiten Schritt auf beiden Seiten der Gleichung 5x und wir erhalten 2x plus 5 ist minus 1.

Im nächsten Schritt werden die variablenfreien Glieder auf die andere Seite der Gleichung gebracht. In unserem Falle dadurch, dass auf beiden Seiten die Zahl 5 subtrahiert wird.

Dritter Rechenschritt

3. Variable Glieder auf die andere Seite bringen

Wir erhalten eine schon sehr vereinfachte Form der Ausgangsgleichung mit 2x ist minus 6. Damit wir die Lösung für 1x direkt ablesen können, dividieren wir im nächsten Rechenschritt beide Gleichungsseiten mit 2. Es ergibt sich x ist minus 3.

Die Lösung

4. Umformung zum Ablesen der Lösung

Während des Lösungsweges entstand eine Kette von äquivalenten Gleichungen. Wegen der Transitivität der Äquivalenz ist auch die letzte Gleichung x ist minus 3 zur ausführlichen Ausgangsgleichung äquivalent. Die Zahl minus 3 ist die einzige Lösung der Gleichung x ist minus 3 und somit auch die einzige Lösung der Ausgangsgleichung. Und daher kann das Lösungselement minus 3 in die Lösungsmenge aufgenommen werden. Dies aber nur, wenn das Lösungselement in der Definitionsmenge, die hier der Grundmenge entspricht, enthalten ist. Da die Zahl minus 3 ein Element der Menge der ganzen Zahlen ist, erhalten wir die Lösungsmenge mit dem Lösungselement minus 3.

Hätten wir als Grundmenge die Menge der natürlichen Zahlen gewählt, so dürften als Lösungselemente nur natürliche Zahlen auftreten. Da die Zahl minus 3 keine natürliche Zahl ist, wäre dann die Lösungsmenge eine leere Menge.

Überprüfung der Richtigkeit

Zur Überprüfung der Richtigkeit der Lösungsmenge gehört zu jeder Gleichung mit Variablen eine Probe. Diese Probe ist immer in der Ausgangsgleichung durchzuführen. Das Lösungselement wird dabei für die Variable eingesetzt. Ergibt sich eine wahre Aussage, so ist das Lösungselement richtig ermittelt worden. Probieren wir dies bei unserem Beispiel mit unserem Lösungselement minus 3. Wie die Probe in unserem Fall im einzelnen verläuft, zeigt Ihnen Heinz Gascha im nachfolgenden Video.