Grundkurs Mathematik (4) 4.1. Gleichungen mit und ohne Variable
Lineare Gleichungen und Ungleichungen sind für die gesamte Mathematik von großer Bedeutung. Nach den Zahlen gehören sie zu den ersten mathematischen Errungenschaften der Menschheit.
Sätze, bei denen ein Teil der Aussage durch eine Leerstelle, mathematisch gesehen durch einen Platzhalter, ersetzt ist, heißen Aussageformen.
Eine Wolke als Platzhalter
Eine Wolke als Platzhalter - klicken Sie bitte auf die Lupe
Nehmen wir eine Wolke als Platzhalter, gewählt ist eine Stadt in Bayern. Um Belegungen für die Leerstelle finden zu können, benötigen wir eine Menge von Städten, aus denen ausgewählt werden darf. Diese Menge wird in der Mathematik als Grundmenge G bezeichnet.
Klicken Sie bitte auf die Lupe
Wählen wir mal die Städte Berlin, Hamburg, Hannover, München und Nürnberg. Jede dieser Städte ist jetzt ein Element unserer Grundmenge und darf zur Belegung der Leerstelle in unserer Aussageform verwendet werden.
Setzen wir Berlin in die Wolke ein, so erhalten wir eine falsche Aussage. Das gilt auch für Hamburg und Hannover. Wählen wir aber München, so ergibt sich eine wahre Aussage, wie auch für die Stadt Nürnberg.
Grundmenge und Lösungsmenge
Alle Elemente aus der Grundmenge G, die beim Einsetzen wahre Aussagen liefern, heißen Lösungen der Aussageform. In unserem Beispiel wäre das neben München auch noch die Stadt Nürnberg. Die Lösungen fasst man zur Lösungsmenge L der Aussageform zusammen.
Darstellung in der Mathematik
In der Mathematik wählt man als Platzhalter kleine lateinische Buchstaben, wie zum Beispiel ein x. Mengen schreibt man in Mengenklammern.
Die Aussageform heißt: x ist eine Stadt in Bayern. Gewählt wird aus der Grundmenge G mit den festgelegten Städten in der Mengenklammer. Als Lösungsmenge ergibt sich die zwei-elementige Menge mit München und Nürnberg, das liefert nämlich die wahren Aussagen.
Aussageformen: Gleichungen und Ungleichungen
Linksterm und Rechtsterm der Gleichung - klicken Sie bitte auf die lupe
In der Mathematik heißen Aussageformen Gleichungen und Ungleichungen. Die Gleichung ist eine Aussageform, in der zwei Terme T eins und T zwei durch das Gleichheitszeichen miteinander verbunden sind. Die beiden Terme bezeichnet man als Linksterm und Rechtsterm der Gleichung. Allgemein kann man also jede Gleichung in der Form T1 als Linksterm ist gleich T2 als Rechtsterm darstellen.
Definitionsbereich und Schnittmenge
Schnittmenge - klicken Sie bitte auf die lupe
Enthalten Linksterm und Rechtsterm mehrere Variable, so ist der Definitionsbereich der Gleichung die Schnittmenge der Definitionsbereiche aller in ihr vorkommenden Terme mit Variablen. Für die einzelnen Terme ist bei der Bestimmung des Definitionsbereiches die jeweilige Grundmenge zu beachten.
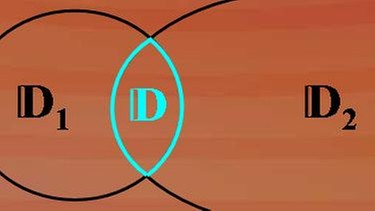
Nehmen wir mal an, unser Linksterm hat eine Definitionsmenge D eins, unser Rechtsterm die Definitionsmenge D zwei. So ist die Definitionsmenge D die Schnittmenge aus den Einzeldefinitionsmengen.
Wahre und falsche Gleichungen
Wie sieht es aber aus, wenn Gleichungen keinen Platzhalter, also keine Variable enthalten? Denn 5 plus 2 ist gleich 7 oder 4 minus 2 ist gleich 8 sind doch auch Gleichungen. Man kann aber sofort erkennen, ob sie wahr oder falsch sind.
Gleichungen ohne Variable:
Gleichungen, deren Terme keine Variable enthalten, sind mathematisch gesehen Aussagen, die entweder wahr oder falsch sind. Es sind also keine Aussageformen.