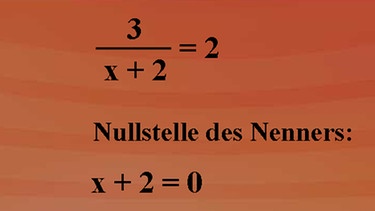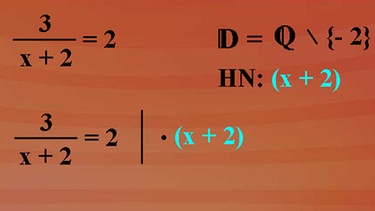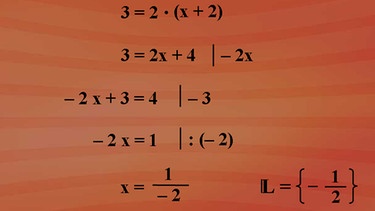Hierzu ein Beispiel:

Beispiel

Bruchgleichung - klicken Sie bitte auf die Lupe

3 geteilt durch x plus 2, also im Nenner x plus 2, gleich2. Und als Grundmenge wählen wir wieder die Menge der rationalen Zahlen Q. Bevor man an die Lösungsmengenbestimmung einer Bruchgleichung gehen kann, müssen alle auftretenden Quotienten, in unserem Falle einer, auf ihre Definiertheit hin untersucht werden. Denn im Nenner eines Quotienten darf nie der Wert Null auftreten. Durch die Angabe einer Definitionsmenge werden Belegungen, für die der Nenner eines Quotienten gleich Null werden kann, ausgeschlossen. In unserem Falle hat der auftretende Quotient den Nenner x+2. Dieser Nenner hat für die Belegung x gleich minus 2 den Wert Null. Für unsere Grundmenge Q lautet dann die Definitionsmenge: D ist die Menge der rationalen Zahlen Q ohne die Menge mit dem Element minus 2.

Lösung einer Bruchgleichung

Lösung einer Bruchgleichung - klicken Sie bitte auf die Lupe

Da nur ein Nennerterm auftritt, bildet dieser zugleich den Hauptnenner, mit dem die Bruchgleichung auf beiden Seiten multipliziert wird. Wir erhalten auf der linken Seite 3 durch x plus 2 mal x plus 2 und rechts 2 mal x plus 2, jeweils in Klammern geschrieben. Auf der linken Seite lässt sich der Term x plus 2 kürzen und wir erhalten die lineare Gleichung 3 ist 2 mal x plus 2 in Klammern. Und das können wir schon lösen. Ausmultipliziert 3 ist 2 mal x plus 2 mal 2 ist 4. x-Glieder auf die linke Seite mit minus 2x liefert minus 2x + 3 ist 4 und auf beiden Seiten 3 subtrahiert ergibt minus 2x gleich 1.

Der letzte Lösungsschritt - klicken Sie bitte auf die Lupe

Um die Lösung für 1x ablesen zu können, teilen wir noch beide Gleichungsseiten mit minus 2 und wir erhalten das Lösungselement minus ein halb. Da das Element minus ein halb in der Definitionsmenge nicht ausgeschlossen ist und zugleich eine rationale Zahl ist, darf es in die Lösungsmenge als Lösungselement aufgenommen werden.