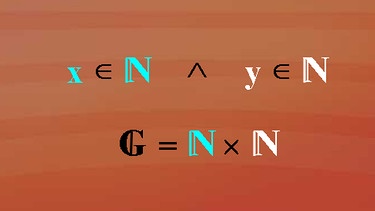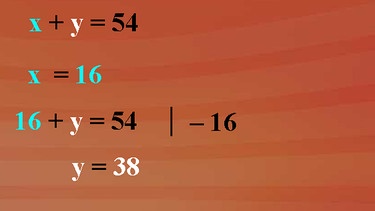Grundkurs Mathematik (5) 5.1. Gleichung mit zwei Unbekannten
Eine lineare Gleichung mit einer Variablen können Sie bereits lösen. Doch was macht man, wenn zwei Variable zu bestimmen sind? Dann reicht eine Gleichung nicht mehr aus ...
Gleichung mit zwei Unbekannten
Stellen Sie sich einfach mal vor, wir bekommen gesagt, dass die Freunde Fritz und Martin zusammen 54 Jahre alt sind, und wir sollen daraus auf das Alter von Fritz schließen. Dies ist nicht eindeutig feststellbar. Setzen wir für das Alter von Fritz die Variable x und für das Alter von Martin die Variable y, so erhalten wir auf Grund der getroffenen Aussage die Aussageform x plus y ist gleich 54.
Aus der letzten Folge wissen wir noch, dass wir für die auftretenden Variablen eine Grundmenge anzugeben haben. Gehen wir davon aus, dass uns die Angabe des Alters in Jahren ausreicht, also 2, 4 oder 6 Monate älter nicht interessieren, so ist für die Variablen x und y jeweils die Menge der natürlichen Zahlen N als Grundmenge ausreichend.
Ein Kreuzzeichen als Verkopplungszeichen
Kreuzzeichen als Verkopplungszeichen - klicken Sie bitte auf die Lupe.
So wird das Verkopplungszeichen mathematisch dargestellt: x Element aus N und zugleich y Element aus N. Dies kann man zur Grundmenge G ist N kreuz N zusammenfassen, wobei das erste N für die x- Belegung und das zweite N für die y- Belegung zuständig ist.
Das gesetzte Kreuzzeichen, das wie ein x aussieht, wird als Verkopplungszeichen für die beiden angegebenen Mengen verwendet. Es ermöglicht die Gesamtdarstellung der Grundmenge. Bei uns jetzt für zwei Variable.
Bei drei Variablen würde sich ein weiteres Kreuz mit beliebiger Menge anschließen. Zum Beispiel N kreuz N kreuz Z, was bedeuten würde, dass die dritte Variable aus der Menge der ganzen Zahlen Z stammt. Und das ist dann beliebig erweiterbar. Wie sie wissen, benötigen wir bei Gleichungen die Angabe der Grundmenge, um eine Lösungsmenge angeben zu können.
Wie alt sind Fritz und Martin?
Rechenbeispiel - klicken Sie bitte auf die Lupe.
Nehmen wir an Fritz ist 16 Jahre alt. Dann erhalten wir als lineare Gleichung mit der Variablen y: 16 plus y ist 54. Nach y aufgelöst y gleich 54 minus 16 ist 38. Somit wäre Martin 38 Jahre alt. Aber Martin könnte auch 20 Jahre alt sein. Dann erhalten wir eine lineare Gleichung mit der Variablen x: x plus 20 ist 54. Und nach x aufgelöst ist gleich 54 minus 20 ist 34. Fritz wäre dann 34 Jahre alt.
Das könnten wir jetzt lustig weiterprobieren. Für 53 Altersmöglichkeiten von Fritz und 53 Altersmöglichkeiten von Martin. Wir können daraus erkennen, dass zur eindeutigen Bestimmung der Variablen x und y noch eine zweite Aussage, dargestellt in einer zweiten Aussageform, fehlt.
Wir brauchen eine zweite Aussageform
Das könnte jetzt eine Angabe sein, die besagt, dass Fritz zwei Jahre älter ist als Martin, oder Martin doppelt so alt ist wie Fritz. Auch die zweite Aussageform muss die Variable der ersten Aussageform in der gleichen Grundmenge enthalten. Die beiden Aussageformen bilden dann ein System.
Grundsatz:
Lineare Gleichungen mit zwei Variablen können nur dann eindeutig gelöst werden, wenn zwei Gleichungen gegeben sind, die ein lineares Gleichungssystem bilden.
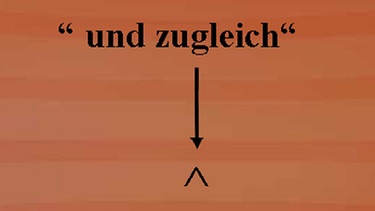
Das Verknüpfungszeichen "und zugleich"
Allgemeine Formel eines Systems linearer Gleichungen mit zwei Gleichungsvariablen - klicken Sie bitte auf die Lupe.
Ein System von linearen Gleichungen mit zwei Gleichungsvariablen hat die allgemeine Form: a eins mal x plus b eins mal y ist gleich c eins als Gleichung I und zugleich a zwei mal x plus b zwei mal y gleich c zwei als Gleichung II. Das Zeichen, welches aussieht wie ein Dach, ist das Verknüpfungszeichen für die beiden Gleichungen und bedeutet "und zugleich". Die Zusammengehörigkeit der beiden Gleichungen wird verdeutlicht durch einen Systemkasten.
Die Grundmenge Q kreuz Q
Grundmenge - klicken Sie bitte auf die Lupe.
Für die Gleichungsvariablen x und y gilt die Grundmenge Q kreuz Q, also x Element aus Q und y Element aus Q. Alle anderen auftretenden Variablen sind sogenannte Formvariable, die als Platzhalter für Zahlen, die aus der Aussage entnommen werden können, gesetzt sind. In unserer allgemeinen Form haben wir für diese Platzhalter Elemente aus der Menge der rationalen Zahlen Q gewählt.
Andere Darstellungsformen
Statt dem Systemkasten wird in der Literatur oftmals auch nur ein Längsstrich am Rande der zusammengehörenden Gleichungen gesetzt. Oder ein Querstrich unter den zusammengehörenden Gleichungen. In anderen Büchern wird auf diese Striche ganz verzichtet und es steht nur das Verknüpfungszeichen "und zugleich".
Lassen Sie sich also davon nicht irritieren.