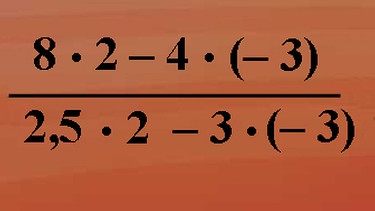Grundkurs Mathematik (5) 5.6. Die "Lösungsformel"
Zu guter Letzt stellen wir noch die "Lösungsformel" vor - ein Verfahren, mit dem auch programmierbare Taschenrechner arbeiten und das immer anzuwenden ist.
Es ist die "Lösungsformel", die für ein allgemeines lineares Gleichungssystem über das Additionsverfahren hergeleitet werden kann. Sie können die Herleitung ihrem Begleitmaterial entnehmen.
Die Formel lautet:
Die Formel - klicken Sie bitte auf die Lupe
Für das allgemeine lineare Gleichungssystem, das wir zu Beginn unserer heutigen Sendung gezeigt haben, lautet das Lösungspaar c eins mal b zwei minus c zwei mal b eins durch a eins mal b zwei minus a zwei mal b eins für die Gleichungsvariable x, sowie a eins mal c zwei minus a zwei mal c eins durch a eins mal b zwei minus a zwei mal b eins für die Gleichungsvariable y. Wobei der Nenner a eins mal b zwei minus a zwei mal b eins nicht gleich Null sein darf.
Anwendung der Formel im Beispiel
Anwendung der Formel - klicken Sie bitte auf die Lupe
Wenden wir diese Formel für unser eben verwendetes Gleichungssystem an, werden sie erkennen, dass es nur noch um einfaches Belegen von Formvariablen geht. Wichtig ist, dass man die Formvariablen richtig zuordnet.
Dann hat man schon gewonnen. Es ist nur noch Spielerei.
Der Weg zur Lösungsmenge - klicken Sie bitte auf die Lupe
Überall wo ein a eins steht wird 2,5 eingesetzt, wo ein b eins steht minus 3, und so mit allen Formvariablen. Ab hier freut sich ihr Freund Taschenrechner, dass er auch wieder mal zum Einsatz kommt.
Es ergibt sich die Lösungsmenge mit dem Lösungspaar 2 und minus 1.
Wie viele Lösungspaare kann es geben?:
Ist das Gleichungssystem eindeutig lösbar, gibt es ein Lösungspaar. Widersprechen die Gleichungen des Systems einander, ergibt es kein Lösungspaar.
Entsprechen die beiden Gleichungen einander, so ergibt es unendlich viele Lösungspaare. Es ist dann so, als hätte man nur eine Gleichung mit zwei Variablen.