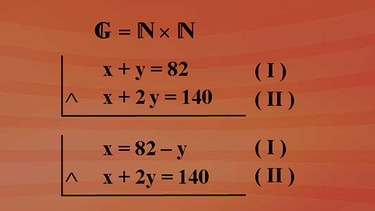Grundkurs Mathematik (5) 5.4. Das Einsetzverfahren
Es gibt noch andere Verfahren - eines ist das Einsetzverfahren: Ein anderer Weg, der genauso zum Ziel führt. Und Gleichungen mit zwei Unbekannten sind kein Problem mehr.
Sehen wir uns dazu das Ausgangssystem nochmals an.
Das Einsetzverfahren im praktischen Beispiel
Auflösen nach x - klicken Sie bitte auf die Lupe
Man kann die erste Gleichung nach der Gleichungsvariablen x auflösen und erhält x gleich 82 minus y. Und diesen Term 82 minus y setzen wir in der zweiten Gleichung für x ein. Somit bekommt man 82 minus y plus 2y ist gleich 140 in der Grundmenge N.
Und wiederum haben wir unser Ziel erreicht. Wir haben aus zwei Gleichungen mit 2 Variablen eine Gleichung mit einer Variablen erhalten. Das Mathematikerherz lacht, denn ab hier ist es nur noch das Lösen einer einfachen linearen Gleichung.
Die Lösung
Die Lösung
Die y- Glieder zusammengefasst ergibt 82 plus y ist 140. Und auf beiden Seiten 82 subtrahiert bekommen wir auch nach diesem Verfahren die Lösung y gleich 58.
Ab hier, das heißt nach der Berechnung der ersten Gleichungsvariablen, kann genauso verfahren werden, wie vorher. Man setzt die Lösung für die eine Gleichungsvariable in eine der beiden Ausgangsgleichungen des Systems ein und kann dadurch die andere Gleichungsvariable ermitteln.
Man nennt dieses jetzt verwendete Verfahren Einsetzverfahren.
Das Einsetzverfahren:
Beim Einsetzverfahren wird ein ganzer Term für eine Variable eingesetzt: Eine Gleichung wird nach einer Variablen aufgelöst, und der für die Variable gefundene Term in die andere Gleichung eingesetzt. Es entsteht somit eine Gleichung mit nur einer Gleichungsvariablen.
Vervollständigen wir noch unser Beispiel:
Das Lösungspaar - klicken Sie bitte auf die Lupe
Wir erhalten auch hier für y in Gleichung I eingesetzt x plus 58 ist 82, mit dem Ergebnis x gleich 24 und der Lösungsmenge L mit dem Lösungspaar 24 und 58.